Вписанная окружность
Если отрезок (луч) принадлежит прямой, касательной к окружности, и точка касания является точкой отрезка (луча), то говорят, что данный отрезок (луч) является касательным к окружности.
Окружность называется вписанной в неразвернутый угол, если она касается сторон этого угла. На рисунке 0 окружности с центрами А и В вписаны в угол МОР, а окружность с центром С нет. Центры всех окружностей, вписанных в угол, равноудалены от его сторон, поэтому принадлежат биссектрисе угла.
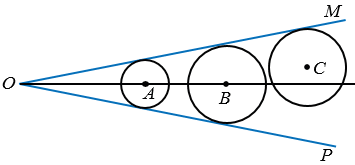
Рис. 0
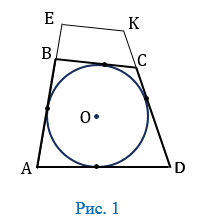
Окружность вписанная в многоугольник - это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник - это многоугольник, в который вписана окружность. На рисунке 1 четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
Теорема
| В любой треугольник можно вписать окружность. |
Доказательство
Дано: произвольный  АВС.
АВС.
Доказать: в  АВС можно вписать окружность.
АВС можно вписать окружность.
Доказательство:
1. Проведем биссектрисы углов А, В и С, которые пересекутся в точке О (следствие из свойства биссектрис). Из точки О проведем перпендикуляры ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА (Рис. 2).
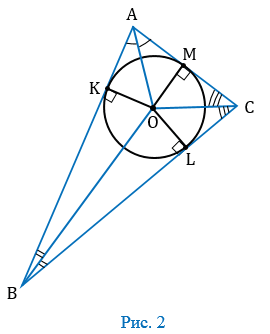
2. Точка О равноудалена от сторон  АВС (свойство биссектрис), поэтому ОК = ОL = ОМ. Следовательно, окружность с центром О радиуса ОК проходит через точки К, L и М. Стороны
АВС (свойство биссектрис), поэтому ОК = ОL = ОМ. Следовательно, окружность с центром О радиуса ОК проходит через точки К, L и М. Стороны  АВС касаются этой окружности в точках К, L, М, т.к. они перпендикулярны к радиусам ОК, ОL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в
АВС касаются этой окружности в точках К, L, М, т.к. они перпендикулярны к радиусам ОК, ОL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в  АВС. Теорема доказана.
АВС. Теорема доказана.
Замечание 1
| В треугольник можно вписать только одну окружность. |
Доказательство
Предположим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудален от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают, значит в треугольник можно вписать только одну окружность. Что и требовалось доказать.
Замечание 2
| Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности. |
Доказательство
На рисунке 2 мы видим, что  АВС составлен из трех треугольников: АВО, ВСО и САО. Пусть АВ, ВС и АС основания треугольников АВО, ВСО и САО соответственно, тогда высотами данных треугольников окажутся отрезки ОК = ОL = ОМ = ( - радиус окружности с центром О). Следовательно, площади этих треугольников вычисляются по формулам:
АВС составлен из трех треугольников: АВО, ВСО и САО. Пусть АВ, ВС и АС основания треугольников АВО, ВСО и САО соответственно, тогда высотами данных треугольников окажутся отрезки ОК = ОL = ОМ = ( - радиус окружности с центром О). Следовательно, площади этих треугольников вычисляются по формулам: 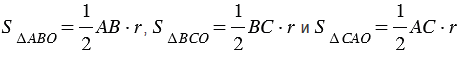 . Тогда, по свойству площадей, площадь треугольника
. Тогда, по свойству площадей, площадь треугольника  АВС выражается формулой:
АВС выражается формулой: 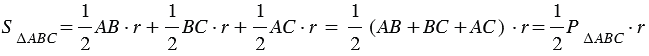 , где
, где 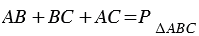 - периметр
- периметр  АВС. Что и требовалось доказать.
АВС. Что и требовалось доказать.
Замечание 3
| Не во всякий четырехугольник можно вписать окружность. |
Доказательство
Рассмотрим, например, прямоугольник, у которого смежные стороны не равны, т.е. прямоугольник, не являющийся квадратом. В такой прямоугольник можно "поместить" окружность, касающуюся трех его сторон (Рис.3), но нельзя "поместить" окружность так, чтобы она касалась всех четырех его сторон, т.к. диаметр окружности меньше большей стороны прямоугольника т.е. нельзя вписать окружность. Что и требовалось доказать.
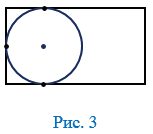
Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:
| В любом описанном четырехугольнике суммы противоположных сторон равны. |
Доказательство
Рассмотрим четырехугольник АВСD, описанный около окружности (Рис. 4).
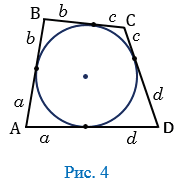
На рисунке 4 одинаковыми буквами обозначены равные отрезки касательных, т.к. отрезки касательных к окружности, проведенные из одной точки, равны. Тогда АВ + СD = 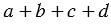 и ВС + АD =
и ВС + АD = 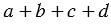 , следовательно, АВ + СD = ВС + АD.
, следовательно, АВ + СD = ВС + АD.
Верно и обратное утверждение:
| Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность. |
Доказательство
Пусть в выпуклом четырехугольнике АВСD
АВ + СD = ВС + АD. (1)
Точка О пересечения биссектрис углов А и В равноудалена от сторон АD, АВ и ВС (свойство биссектрис), поэтому можно провести окружность с центром О, касающуюся указанных трех сторон (Рис. 5).
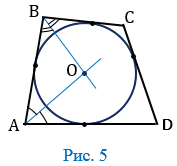
Докажем, что эта окружность касается также стороны СD и, значит, является вписанной в четырехугольник АВСD.
Предположим, что это не так. Тогда прямая СD либо не имеет общих точек с окружностью, либо является секущей. Рассмотрим первый случай (Рис. 6). Проведем касательную С1D1, параллельную стороне СD (С1 и D1 - точки пересечения касательной со сторонами ВС и АD).
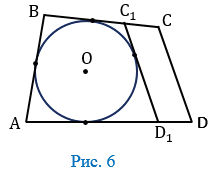
Так как АВС1D1 - описанный четырехугольник, то по свойству его противоположных сторон
АВ + С1D1 = ВС1 + AD1. (2)
Но ВС1 = ВС - С1С, АD1 = АD - D1D, поэтому из равенства (2) получаем:
С1D1 + С1С + D1D = ВС + АD - АВ.
Правая часть этого равенства в силу (1) равна СD. Следовательно, приходим к равенству
С1D1 + С1С + D1D = СD,
т.е. в четырехугольник С1СDD1 одна сторона равна сумме трех других сторон. Но этого не может быть, т.к. каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон. Значит, наше предположение ошибочно. Аналогично можно доказать, что прямая CD не может быть секущей окружности. Следовательно, окружность касается стороны СD. Что и требовалось доказать.
Советуем посмотреть:
Свойства диаметров и хорд окружности
Взаимное расположение прямой и окружности
Взаимное расположение двух окружностей
Общие касательные двух окружностей
Градусная мера дуги окружности
Углы, образованные хордами, касательными и секущими
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 689, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 692, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 694, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 701, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 722, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 734, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1105, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1281, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 371, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 820, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник