Четырехугольник

Четырехугольник - это многоугольник, который имеет четыре вершины (А, В, С, D), четыре стороны (АВ, BC, CD, AD) и две диагонали (АС, ВD) (рис.1).

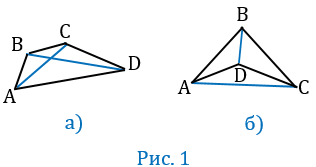
Две несмежные стороны четырехугольника называются противоположными. Две вершины, не являющиеся соседними, также называются противоположными.

Периметр четырехугольника (Р) - это сумма длин четырех его сторон. Периметр четырехугольника изображенного на рисунке 1,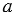 равен сумме длин АВ, ВС, СD и АD, т.е. Р = АВ + ВС + СD + АD.

Четырехугольники бывают выпуклые (рис.1,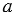) и невыпуклые (рис.1, б).

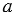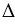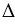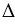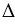Каждая диагональ выпуклого четырехугольника разделяет его на два треугольника. На рисунке 1, диагональ ВD разбивает выпуклый четырехугольник АВСD на АВD и ВСD, а диагональ АС - на АВС и АСD.

Сумма углов выпуклого и невыпуклого n-угольников равна (n-2)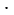180⁰, тогда, учитывая то, что у четырехугольника 4 угла, т.е. n = 4, сумма углов выпуклого и невыпуклого четырехугольников равна (4-2)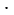180⁰ = 360⁰.