Свойство биссектрисы угла
Теорема
|
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе. |
Доказательство
1) Дано: 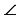 ВАС, АМ - биссектриса, МК
ВАС, АМ - биссектриса, МК 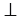 АВ, ML
АВ, ML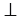 АС.
АС.
Доказать: MK = ML
Доказательство:
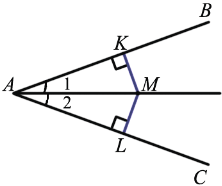
Рассмотрим 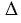 АМК и
АМК и 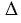 AML: МК
AML: МК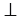 АВ, ML
АВ, ML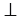 АС, поэтому рассматриваемые треугольники прямоугольные. АМ - общая гипотенуза,
АС, поэтому рассматриваемые треугольники прямоугольные. АМ - общая гипотенуза, 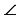 1 =
1 = 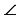 2, т.к. луч АМ - биссектриса, следовательно,
2, т.к. луч АМ - биссектриса, следовательно, 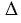 АМК =
АМК = 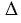 AML, по гипотенузе и острому углу, а в равных треугольниках против соответственно равных углов лежат равные стороны, поэтому MK = ML.
AML, по гипотенузе и острому углу, а в равных треугольниках против соответственно равных углов лежат равные стороны, поэтому MK = ML.
2) Дано: 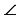 ВАС, MK = ML, МК
ВАС, MK = ML, МК 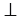 АВ, ML
АВ, ML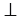 АС.
АС.
Доказать: АМ - биссектриса 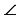 ВАС
ВАС
Доказательство:

Рассмотрим 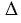 АМК и
АМК и 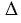 AML: МК
AML: МК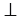 АВ, ML
АВ, ML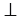 АС, поэтому рассматриваемые треугольники прямоугольные. АМ - общая гипотенуза, MK = ML по условию, следовательно,
АС, поэтому рассматриваемые треугольники прямоугольные. АМ - общая гипотенуза, MK = ML по условию, следовательно, 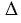 АМК =
АМК = 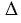 AML, по гипотенузе и катету, а в равных треугольниках против соответственно равных сторон лежат равные углы, поэтому
AML, по гипотенузе и катету, а в равных треугольниках против соответственно равных сторон лежат равные углы, поэтому 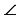 1 =
1 = 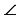 2, а это означает, что луч АМ - биссектриса
2, а это означает, что луч АМ - биссектриса 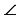 ВАС. Теорема доказана.
ВАС. Теорема доказана.
Следствие 1
| Геометрическим местом точек плоскости, лежащих внутри неразвёрнутого угла и равноудалённых от сторон угла, является биссектриса этого угла. |
Следствие 2
| Биссектрисы треугольника пересекаются в одной точке. |
В самом деле, обозначим буквой О точку пересечения биссектрис АА1 и ВВ1 треугольника АВС и проведем перпендикуляры ОК, OL и ОМ соответственно к прямым АВ, ВС и СА.
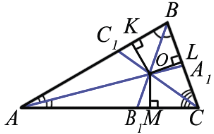
По доказанной теореме ОК = ОМ и ОК = OL. Поэтому ОМ = OL, т.е. точка О равноудалена от сторон угла АСВ и, значит, лежит на биссектрисе СС1 этого угла. Следовательно, все три биссектрисы треугольника АВС пересекаются в точке О, что и требовалось доказать.
Советуем посмотреть:
Свойства диаметров и хорд окружности
Взаимное расположение прямой и окружности
Взаимное расположение двух окружностей
Общие касательные двух окружностей
Градусная мера дуги окружности
Углы, образованные хордами, касательными и секущими
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 677, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 688, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 707, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 724, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1086, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1275, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 16, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 22, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 458, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 757, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник