Задание 366 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№366 учебника 2013-2022 (стр. 100):
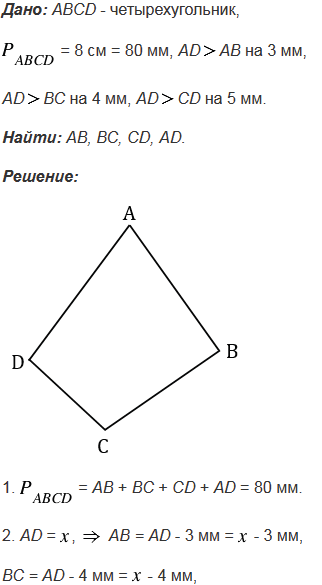
Найдите стороны четырехугольника, если его периметр равен 8 см, а одна сторона больше каждой из других сторон соответственно на 3 мм, 4 мм и 5 мм.
№366 учебника 2023-2024 (стр. 105):
Подсказка
№366 учебника 2013-2022 (стр. 100):
Вспомните:
- Какая фигура называется четырехугольником, его периметр.
№366 учебника 2023-2024 (стр. 105):
Вспомните:
- Какой треугольник называют равносторонним.
- Свойства равностороннего треугольника.
- Элементы окружности.
- Какую окружность называют описанной около треугольника.
- Какую окружность называют вписанной в треугольник.
- Что называют серединным перпендикуляром к отрезку.
- Что называют биссектрисой, высотой, медианой треугольника.
Ответ
№366 учебника 2013-2022 (стр. 100):


№366 учебника 2023-2024 (стр. 105):
Дано: окружность вписанная и окружность описанная около равностороннего  АВС.
АВС.
Доказать: центры вписанной и описанной окружностей совпадают.
Доказательство:
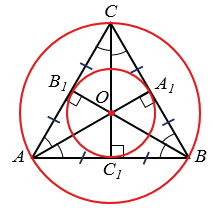
Центром окружности вписанной в треугольник является точка пересечения серединных перпендикуляров к сторонам треугольника.
Центром окружности описанной около треугольника является точка пересечения биссектрис этого треугольника.
В равностороннем треугольнике, биссектрисы являются и медианами и высотами, значит, они являются и серединными перпендикулярами, следовательно, центры вписанной и описанной окружностей около равностороннего треугольника совпадают. Что и требовалось доказать.
Пояснения:
Вернуться к содержанию учебника