Взаимное расположение двух окружностей
Концентрические окружности - окружности с общим центром и различными радиусами. На рисунке 1 окружности с центрами О1 и О2 и радиусами R и r соответственно - концентрические окружности.
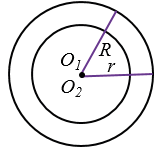
Рис. 1
Концентрические окружности не имеют общих точек, все точки одной из окружностей являются внутренними точками относительно другой.
Заметим, что две окружности с разными центрами не могут иметь более двух общих точек.
Рассмотрим окружности, у которых центры О1 и О2 не совпадают. Пусть d расстояние между точками О1 и О2. Для определенности будем считать, что R 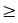 r.
r.
Если окружности имеют две общие точки, то говорят, что они пересекаются. На рисунках 2 а, б окружности пересекаются в двух точках М1 и М2. Обратите внимание, в этом случае d < R + r или d > R - r.
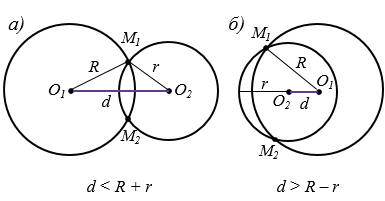
Рис. 2
Если две окружности имеют одну общую точку, то говорят, что они касаются. Общая точка окружностей в этом случае называется точкой касания. На рисунке 3, 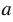 окружности касаются внутренним образом, в этом случае d = R - r. На рисунке 3, б окружности касаются внешним образом, в этом случае d = R + r.
окружности касаются внутренним образом, в этом случае d = R - r. На рисунке 3, б окружности касаются внешним образом, в этом случае d = R + r.
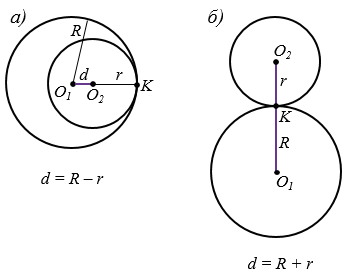
Рис. 3
На рисунке 4, 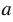 все точки окружности с центром О2 являются внутренними точками относительно окружности с центром О1. В таком случае говорят, что одна окружность лежит внутри другой, при этом d < R - r. На рисунке 4, б окружности не имеют общих точек и ни одна из них не лежит внутри другой. В таком случае говорят, что окружность с центром О2 лежит вне окружности с центром О1, при этом d > R + r.
все точки окружности с центром О2 являются внутренними точками относительно окружности с центром О1. В таком случае говорят, что одна окружность лежит внутри другой, при этом d < R - r. На рисунке 4, б окружности не имеют общих точек и ни одна из них не лежит внутри другой. В таком случае говорят, что окружность с центром О2 лежит вне окружности с центром О1, при этом d > R + r.
Рис. 4
Лемма
Если для длин  , ,  и и 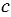 трех данных отрезков выполняются условия: трех данных отрезков выполняются условия: 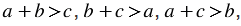 то существует треугольник, стороны которого равны данным отрезкам. то существует треугольник, стороны которого равны данным отрезкам. |
Теорема о взаимном расположении двух окружностей
|
Пусть центры О1 и О2 двух окружностей с радиусами R и r не совпадают, О1О2 = d, тогда: 1) окружности пересекаются, если R - r < d < R + r и R 2) окружности касаются внешним образом, если d = R + r; 3) окружности касаются внутренним образом, если d = R - r и R > r; 4) окружности не имеют общих точек, причем окружность с центром О2 расположена вне окружности с центром О1, если d > R + r; 5) окружности не имеют общих точек, причем окружность с центром О2 расположена внутри окружности с центром О1, если d < R - r и R > r. |
Следствие
|
Если две окружности с центрами О1 и О2 пересекаются, то точки их пересечения не лежат на прямой О1О2. Если окружности с центрами О1 и О2 касаются, то точка касания лежит на прямой О1О2. |
Советуем посмотреть:
Свойства диаметров и хорд окружности
Взаимное расположение прямой и окружности
Общие касательные двух окружностей
Градусная мера дуги окружности
Углы, образованные хордами, касательными и секущими
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 739, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 752, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 754, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 756, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 758, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 760, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 798, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 801, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 803, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник