Взаимное расположение прямой и окружности
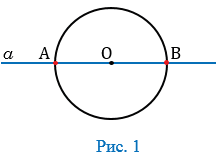
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках - концах диаметра, лежащего на на этой прямой. На рисунке 1 прямая  проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
Если прямая  не проходит через центр О окружности радиуса
не проходит через центр О окружности радиуса  , то возможны три случая взаимного расположения прямой и окружности в зависимости от соотношения между радиусом
, то возможны три случая взаимного расположения прямой и окружности в зависимости от соотношения между радиусом  этой окружности и расстоянием
этой окружности и расстоянием 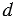 от центра окружности до прямой
от центра окружности до прямой  .
.
1 случай
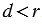 . На прямой
. На прямой  от точки Н отложим два отрезка НА и НВ, длины которых равны
от точки Н отложим два отрезка НА и НВ, длины которых равны 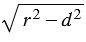 . Точки А и В по построению лежат на одной прямой
. Точки А и В по построению лежат на одной прямой  (Рис.2).
(Рис.2).
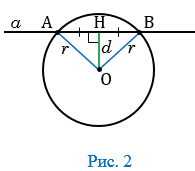
Проверим, лежат ли точки А и В на окружности.
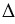 АНО и
АНО и 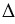 ВНО - прямоугольные (т.к. расстояние
ВНО - прямоугольные (т.к. расстояние 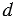 от точки О до прямой
от точки О до прямой  - это перпендикуляр) , следовательно, по теореме Пифагора:
- это перпендикуляр) , следовательно, по теореме Пифагора: 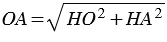 и
и 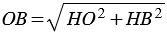 , учитывая то, что ОН =
, учитывая то, что ОН = 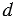 , НА = НВ =
, НА = НВ = 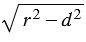 , получим:
, получим:
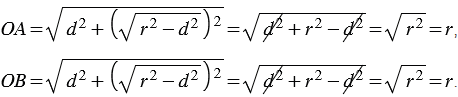
Поэтому точки А и В лежат на окружности и, значит, являются общими точками прямой  и данной окружности,.
и данной окружности,.
Докажем, что прямая  и данная окружность не имеют других общих точек. Предположим, что они имеют еще одну общую точку С, значит, ОС =
и данная окружность не имеют других общих точек. Предположим, что они имеют еще одну общую точку С, значит, ОС =  (Рис.3).
(Рис.3).
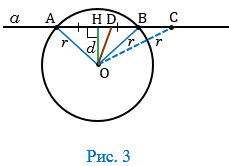
Тогда медиана ОD равнобедренного  ОАС (ОА = ОС =
ОАС (ОА = ОС =  ), проведенная к основанию АС, является высотой этого треугольникам (по свойству равнобедренного треугольника), поэтому OD
), проведенная к основанию АС, является высотой этого треугольникам (по свойству равнобедренного треугольника), поэтому OD 
 . Отрезки ОD и ОН не совпадают, т.к. середина D отрезка АС не совпадает с точкой Н - серединой отрезка АВ. Мы получили, что из точки О проведены два перпендикуляра (отрезки ОН и ОD) к прямой
. Отрезки ОD и ОН не совпадают, т.к. середина D отрезка АС не совпадает с точкой Н - серединой отрезка АВ. Мы получили, что из точки О проведены два перпендикуляра (отрезки ОН и ОD) к прямой  , что невозможно (т.к. из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один). Следовательно, наше предположение неверно, т.е. точка С не является общей точкой прямой
, что невозможно (т.к. из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один). Следовательно, наше предположение неверно, т.е. точка С не является общей точкой прямой  и данной окружности.
и данной окружности.
Вывод:
Если расстояние от центра окружности до прямой меньше радиуса окружности (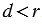 ), то прямая и окружность имеют две общие точки. ), то прямая и окружность имеют две общие точки. |
В этом случае прямая называется секущей по отношению к окружности (на рисунке 2 прямая  - секущая).
- секущая).
2 случай
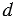 =
=  . В этом случае ОН =
. В этом случае ОН =  , т.е. точка Н лежит на окружности и, значит, является общей точкой прямой и окружности (Рис.4).
, т.е. точка Н лежит на окружности и, значит, является общей точкой прямой и окружности (Рис.4).
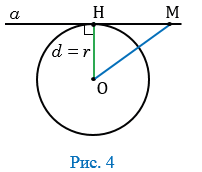
Прямая  и окружность не имеют других общих точек, т.к. для любой точки М прямой
и окружность не имеют других общих точек, т.к. для любой точки М прямой  , отличной от точки Н, ОМ
, отличной от точки Н, ОМ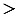 ОН =
ОН =  (наклонная ОМ всегда больше перпендикуляра ОН), и, следовательно, точка М не лежит на окружности.
(наклонная ОМ всегда больше перпендикуляра ОН), и, следовательно, точка М не лежит на окружности.
Вывод:
Если расстояние от центра окружности до прямой равно радиусу окружности (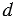 = =  ), то прямая и окружность имеют только одну общую точку. ), то прямая и окружность имеют только одну общую точку. |
В этом случае прямая называется касательной по отношению к окружности (на рисунке 4 прямая  - касательная).
- касательная).
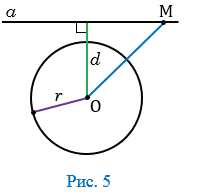
3 случай
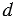
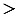
 . В этом случае, ОН
. В этом случае, ОН 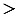
 , поэтому для любой точки М прямой
, поэтому для любой точки М прямой  ОМ
ОМ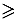 ОН
ОН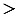
 (Рис. 5). Следовательно, точка М не лежит на окружности.
(Рис. 5). Следовательно, точка М не лежит на окружности.
Вывод:
Если расстояние от центра окружности до прямой больше радиуса окружности (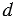 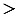  ), то прямая и окружность не имеют общих точек. ), то прямая и окружность не имеют общих точек. |
Советуем посмотреть:
Свойства диаметров и хорд окружности
Взаимное расположение двух окружностей
Общие касательные двух окружностей
Градусная мера дуги окружности
Углы, образованные хордами, касательными и секущими
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 658, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 670, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 2, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 4, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1065, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 1066, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 1361, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник