Сравнение углов

Мы знаем, что геометрические фигуры можно сравнивать методом наложения, а угол - это геометрическая фигура, следовательно, сравнить углы мы можем, наложив один угол на другой.

Рассмотрим два неразвёрнутых угла LOK и BAC

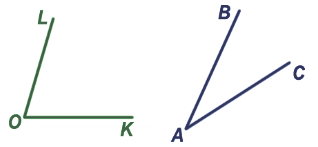
Совместим их вершины (точка O и точка A).

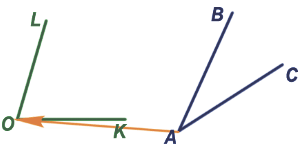
Затем повернём BAC так, чтобы сторона AC совпала со стороной OK, при этом стороны OL и AB должны быть по одну сторону от совпавших сторон.

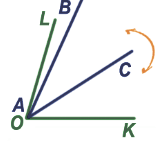
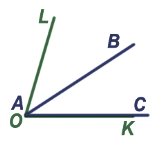
Мы видим, что BAC составляет только часть LOK, следовательно, LOK > BAC.

Если LOB = BOK, то луч OB называется биссектрисой угла.

Теперь сравним LOK и TNS.

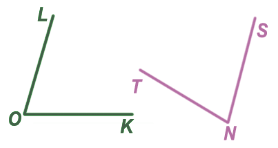
Совместим их вершины (точка O и точка N).

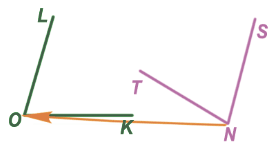
Затем повернём TNS так, чтобы сторона NS совпала со стороной OK, при этом стороны OL и NT должны быть по одну сторону от совпавших сторон.

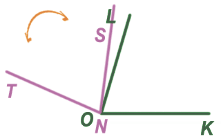
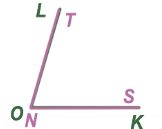
Мы видим, что стороны OL и NT также совпали, следовательно, LOK = TNS.

Неразвёрнутый угол всегда составляет часть развёрнутого угла, следовательно, развёрнутый угол больше любого неразвёрнутого угла.

Пример:

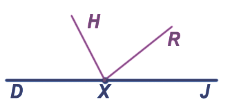
DXJ - развёрнутый угол, HXJ, RXJ, HXD, RXD, HXR - неразвёрнутые углы, и все они составляют лишь часть DXJ и все они меньше его.

Очевидно, что любые два развёрнутых угла равны друг другу.

• Угол, который составляет часть другого угла, считается меньшим.
• Если при наложении одного угла на другой, совпадают обе стороны данных углов, то они равны.
• Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
• Развёрнутый угол больше любого неразвёрнутого угла.
• Любые два развёрнутых угла равны друг другу.