Касательная к окружности
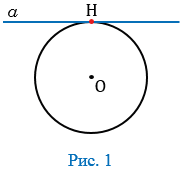
Касательная к окружности - прямая, имеющая с окружностью одну общую точку, которая называется точкой касания прямой и окружности. На рисунке 1 прямая  - касательная к окружности, точка Н - точка касания прямой
- касательная к окружности, точка Н - точка касания прямой  и окружности с центром в точке О.
и окружности с центром в точке О.
Свойство касательной к окружности
Теорема
| Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. |
Доказательство
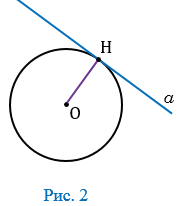
Дано:  - касательная к окружности с центром в точке О, Н - точка касания (Рис. 2).
- касательная к окружности с центром в точке О, Н - точка касания (Рис. 2).
Доказать: ОН
 .
.
Доказательство:
Предположим, что ОН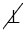
 . Тогда радиус ОН является наклонной к прямой
. Тогда радиус ОН является наклонной к прямой  . При этом перпендикуляр, проведенный из точки О к прямой
. При этом перпендикуляр, проведенный из точки О к прямой  , меньше наклонной ОН, тогда расстояние от центра О окружности до прямой
, меньше наклонной ОН, тогда расстояние от центра О окружности до прямой  меньше радиуса. Следовательно прямая
меньше радиуса. Следовательно прямая  и окружность будут иметь две общие точки, что противоречит условию: прямая
и окружность будут иметь две общие точки, что противоречит условию: прямая  - касательная. Поэтому наше предположение неверно, значит, ОН
- касательная. Поэтому наше предположение неверно, значит, ОН 
 . Теорема доказана.
. Теорема доказана.
| Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. |
Доказательство
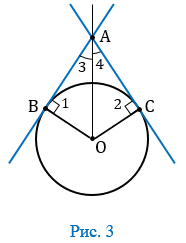
Дано: АВ и АС - касательные к окружности с центром в точке О, В и С - точки касания (Рис. 3).
Доказать: АВ = АС и  3 =
3 = 4.
4.
Доказательство:
 1 =
1 = 2 = 900, т.к. ОВ
2 = 900, т.к. ОВ АВ, ОС
АВ, ОС АС по теореме о свойстве касательной (смотри выше), поэтому
АС по теореме о свойстве касательной (смотри выше), поэтому 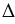 АВО и
АВО и 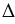 АСО прямоугольные. При этом ОВ = ОС (радиусы), АО - общая, следовательно,
АСО прямоугольные. При этом ОВ = ОС (радиусы), АО - общая, следовательно, 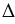 АВО =
АВО =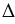 АСО (по гипотенузе и катету). Из равенства треугольников следует, что АВ = АС и
АСО (по гипотенузе и катету). Из равенства треугольников следует, что АВ = АС и  3 =
3 = 4. Что и требовалось доказать.
4. Что и требовалось доказать.
Теорема, обратная теореме о свойстве касательной (признак касательной)
Теорема
| Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной. |
Доказательство
Дано: ОН - радиус окружности с центром в точке О, Н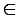
 , ОН
, ОН
 (Рис. 4).
(Рис. 4).
Доказать:  - касательная.
- касательная.
Доказательство:
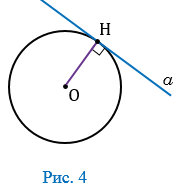
По условию радиус ОН 
 , поэтому расстояние от центра окружности до прямой
, поэтому расстояние от центра окружности до прямой  равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку, значит, данная прямая является касательной к окружности (по определению касательной). Теорема доказана.
равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку, значит, данная прямая является касательной к окружности (по определению касательной). Теорема доказана.
Задача
Через данную точку А окружности с центром О провести касательную к этой окружности.
Дано: точка А лежит на окружности с центром в точке О.
Провести касательную  к окружности так, что А
к окружности так, что А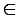
 .
.
Решение:
Строим с помощью циркуля окружность с центром в точке О, отмечаем на данной окружности точку А.
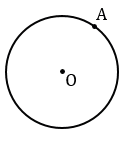
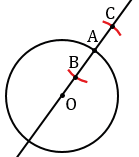
Далее проводим прямую ОА и строим прямую  , проходящую через точку А перпендикулярно к прямой ОА. Для этого с помощью циркуля строим окружность произвольного радиуса с центром в точке А (всю окружность строить необязательно, смотри выделенное красным). Точки пересечения данной окружности с прямой ОА обозначаем буквами В и С.
, проходящую через точку А перпендикулярно к прямой ОА. Для этого с помощью циркуля строим окружность произвольного радиуса с центром в точке А (всю окружность строить необязательно, смотри выделенное красным). Точки пересечения данной окружности с прямой ОА обозначаем буквами В и С.
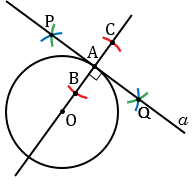
Затем строим две окружности радиуса ВС с центрами в точках В и С (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Данные окружности пересекаются в двух точках, обозначим их Р и Q. Через точки Р и Q с помощью линейки проводим прямую  , которая будет перпендикулярна к прямой ОА.
, которая будет перпендикулярна к прямой ОА.
Итак, 
 ОА, ОА - радиус, следовательно,
ОА, ОА - радиус, следовательно,  - искомая касательная к окружности с центром в точке О радиуса ОА (по признаку касательной).
- искомая касательная к окружности с центром в точке О радиуса ОА (по признаку касательной).
Советуем посмотреть:
Свойства диаметров и хорд окружности
Взаимное расположение прямой и окружности
Взаимное расположение двух окружностей
Общие касательные двух окружностей
Градусная мера дуги окружности
Углы, образованные хордами, касательными и секущими
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 637, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 642, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 647, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 671, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 694, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 347, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 349, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 899, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 1355, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник