Луч

Луч - геометрическая фигура 

Построим прямую АВ 

(прямая обозначена двумя большими латинскими буквами, например, А и В)

Отметим на прямой АВ точку О

Точка О разбивает прямую АВ на две части (влево от точки О и вправо от точки О)

Части, на которые точка О разбивает прямую АВ, выделены цветом

Каждая из этих частей называется лучом, а точка О является началом одного и другого луча

Назовем получившиеся лучи:

Луч ОА, точка О - начало луча ОА; конца у луча ОА нет

Луч ОВ, точка О - начало луча ОВ; конца у луча ОВ нет

Луч является геометрической фигурой

Луч - это часть прямой, ограниченная с одной стороны

Луч имеет начало, но не имеет конца

Другой способ обозначений

Построим прямую m

(прямая обозначена малой латинской буквой, например, m)

Точка О разбивает прямую m на два луча

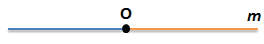
Чтобы лучи обозначить, отметим на прямой m дополнительно произвольным образом две точки - А и В

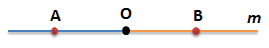
Назовем получившиеся лучи

Луч ОА, точка О - начало луча ОА; конца у луча ОА нет; точка А принадлежит лучу ОА;  

Луч ОВ, точка О - начало луча ОВ; конца у луча ОВ нет; точка В принадлежит лучу ОВ;

Варианты обозначения лучей

1)

Луч ОВ (обозначение двумя большими латинскими буквами)

Точка О - начало луча; В - любая точка на луче ОВ (точка не отмечена)

2)

Луч ОВ (обозначение двумя большими латинскими буквами)

Точка О - начало луча; В - произвольная точка на луче ОВ (точка отмечена)

3)

Луч k (обозначение малой латинской буквой)

Начало луча обозначено буквой О

4)

Луч k (обозначение малой латинской буквой)

Начало луча не обозначено буквой (только отмечено точкой)

Дополнительные лучи

Лучи ОА и ОВ принадлежат одной прямой АВ

Лучи ОА и ОВ имеют общее начало (точка О)

Лучи ОА и ОВ противоположно направлены

При таких условиях лучи ОА и ОВ называются дополнительными