Свойства диаметров и хорд окружности / Окружность / Справочник по геометрии 7-9 класс

Нам уже известно, что окружность - это геометрическая фигура, которая состоит из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Данная точка - центр окружности, а заданное расстояние - радиус окружности. Из определения получается, что окружность представляет собой геометрическое место точек, равноудаленных от центра.

Окружность разбивает множество точек плоскости, не принадлежащих ей, на две части — внутреннюю и внешнюю. Внутренней части принадлежат те точки, для которых расстояние от центра окружности меньше радиуса, а внешней части — те точки, для которых расстояние от центра больше радиуса. Точки внутренней части называют внутренними (точки Е, Р, K и О на рис. 1), а точки внешней части — внешними относительно окружности (точки D, N и M на рис. 1).

Рис. 1

1⁰. Диаметр, проведённый через середину хорды, перпендикулярен этой хорде.

Обратно: диаметр, перпендикулярный хорде, делит её пополам

Доказательство:

1) Пусть диаметр СD окружности с центром О радиуса 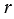проходит через середину Е хорды АВ (рис. 2, 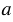). Докажем, что диаметр СD перпендикулярен хорде АВ.

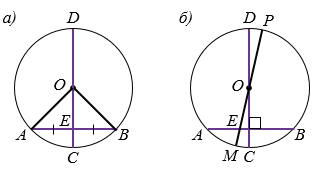
Рис. 2

АОВ - равнобедренный, т.к. ОА и ОВ - радиусы окружности, и отрезок ОЕ - его медиана. В равнобедренном треугольнике медиана, проведенная к основанию, является также высотой треугольника. Значит, ОЕ перпендикулярен АВ.

2) Пусть теперь диаметр СD данной окружности перпендикулярен хорде АВ, и докажем, что он делит хорду пополам.

Рассмотрим диаметр МР, проходящий через середину Е хорды АВ (рис. 2, б). По доказанному выше, отрезки МР и АВ перпендикулярны. Но тогда через центр О окружности проходят две прямые СD и МР, перпендикулярные АВ, значит, они совпадают. Поэтому МР и CD - один и то же диаметр.

Если угол АСВ - прямой, то говорят, что отрезок АВ виден под прямым углом из точки С.

2⁰. Каждая точка, из которой диаметр окружности виден под прямым углом, лежит на этой окружности.

Обратно: из каждой точки окружности любой диаметр, не проходящий через данную точку, виден под прямым углом

Доказательство:

1) Пусть АВ - диаметр окружности с центром О. Тогда если для точки С угол АСВ прямой, то в прямоугольном треугольнике АСВ медиана СО равна половине гипотенузы, к которой она проведена. Тогда ОА = ОВ = ОС, т.е. С лежит на окружности с центром О радиуса ОА.

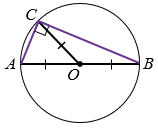
Рис. 3

2) Пусть точка С лежит на окружности с диаметром АВ, О - центр этой окружности (рис. 3). Тогда точка О - середина отрезка АВ. В АСВ медиана СО равна половине стороны, к которой она проведена, поэтому угол АСВ прямой.

Согласно доказанному можно определить еще одно геометрическое место точек: множество всех точек, из которых данный отрезок АВ виден под прямым углом, есть окружность с диаметром АВ (за исключением точек А и В).

Свойства диаметров и хорд окружности

Советуем посмотреть: