Площадь треугольника
Одну из сторон треугольника часто называют основанием. Если основание выбрано, то под словом "высота" подразумевают высоту треугольника, проведенную к основанию.
Теорема
| Площадь треугольника равна половине произведения его основания на высоту |
Доказательство
Дано:  АВС, СН - высота, S - площадь
АВС, СН - высота, S - площадь  АВС
АВС
Доказать: S = 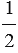 АВ
АВ  СН
СН
Доказательство:
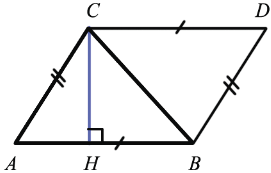
Достроим данный треугольник до параллелограмма ABCD так, как показано на рисунке.  АВС =
АВС =  DCB (по трем сторонам (ВС - общая, AB = CD и АС = BD как противоположные стороны параллелограмма ABCD)), а у равных многоугольников равные площади, значит площади данных треугольников равны. Следовательно, площадь S - площадь
DCB (по трем сторонам (ВС - общая, AB = CD и АС = BD как противоположные стороны параллелограмма ABCD)), а у равных многоугольников равные площади, значит площади данных треугольников равны. Следовательно, площадь S - площадь  АВС равна половине площади параллелограмма ABCD, т.е. S =
АВС равна половине площади параллелограмма ABCD, т.е. S = 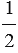 АВ
АВ  СН. Теорема доказана.
СН. Теорема доказана.
Следствие 1
| Площадь прямоугольного треугольника равна половине произведения его катетов |
Следствие 2
| Если высоты двух треугольников равны, то их площади относятся как основания |
Теорема
| Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы |
Доказательство
Дано:  АВС, СН - высота, S - площадь
АВС, СН - высота, S - площадь  АВС,
АВС,  А1В1С1, В1Н1 - высота, S1 - площадь
А1В1С1, В1Н1 - высота, S1 - площадь  А1В1С1,
А1В1С1, 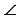 А =
А = 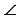 А1
А1
Доказать: 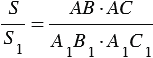
Доказательство:
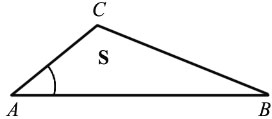
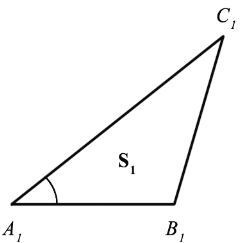
Наложим треугольник А1В1С1 на треугольник АВС так, чтобы вершина А1 совместилась с вершиной А, а стороны А1В1 и А1С1 наложились соответственно на лучи АВ и АС.
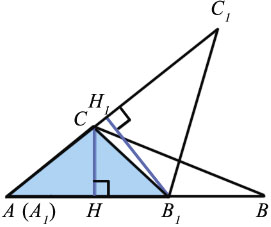
Треугольники АВС и АВ1С имеют общую высоту СН, поэтому
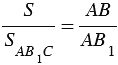
Треугольники АВ1С и АВ1С1 также имеют общую высоту - В1Н1, поэтому
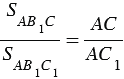
Перемножая полученные равенства, находим:
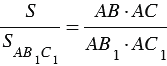 или
или 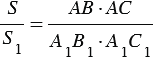
Теорема доказана.
Советуем посмотреть:
Понятие площади многоугольника
Теорема, обратная теореме Пифагора
Правило встречается в следующих упражнениях:
7 класс
Задание 490, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 492, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 517, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 525, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 526, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 571, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 598, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 625, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 830, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 638, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Упражнение 561, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 595, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 613, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс