Углы, образованные хордами, касательными и секущими
Теорема 1
| Угол между хордами окружности измеряется полусуммой двух дуг этой окружности, заключённых между сторонами угла и их продолжениями (рис. 1). |
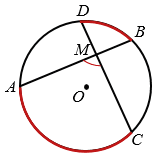
Рис.1
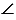 АМС =
АМС = 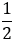 (
(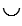 АС +
АС +  ВD)
ВD)
Теорема 2
|
Угол между секущими окружности, пересекающимися в точке, внешней относительно этой окружности, измеряется полуразностью двух дуг этой окружности, заключённых внутри угла (рис. 2)
|
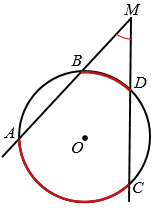
Рис. 2
 АМС =
АМС = 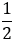 (
(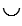 АС -
АС - 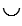 ВD)
ВD)
Теорема 3
|
Угол между хордой и касательной к окружности измеряется половиной дуги этой окружности, заключённой внутри угла (рис.3)
|
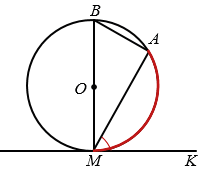
Рис. 3
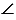 АМK =
АМK = 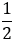
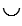 АM
АM
Теорема 4
|
Угол между касательной к окружности и секущей, не проходящей через точку касания, измеряется полуразностью дуг этой окружности, на которые точкой касания делится дуга, заключённая внутри этого угла (рис.4)
|
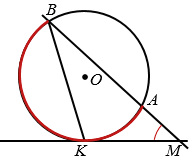
Рис. 4
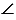 ВМK =
ВМK = 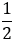 (
(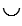 BK -
BK - 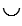 AK)
AK)
Советуем посмотреть:
Свойства диаметров и хорд окружности
Взаимное расположение прямой и окружности
Взаимное расположение двух окружностей
Общие касательные двух окружностей
Градусная мера дуги окружности
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 783, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 801, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 802, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 821, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 822, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 823, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 14, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник