Треугольник
Треугольник - это геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, последовательно соединяющих эти точки. Указанные точки называются вершинами треугольника, а отрезки - сторонами.
Пример: Отметим точки A, B и C, которые не лежат на одной прямой.
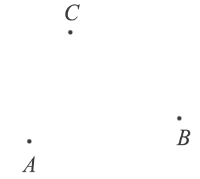
Соединим данные точки отрезками
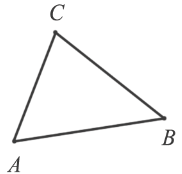
Получившаяся фигура называется треугольником, обозначается 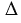 ABC (читается: "треугольник ABC"). Данный треугольник также можно обозначить
ABC (читается: "треугольник ABC"). Данный треугольник также можно обозначить 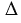 BCA,
BCA, 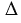 CBA и т.д.
CBA и т.д.
Вершины треугольника: A, B, C.
Углы треугольника: 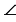 BAC,
BAC, 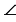 CBA,
CBA, 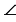 ACB (или их можно обозначать одной буквой
ACB (или их можно обозначать одной буквой 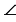 A,
A, 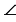 B,
B, 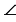 C - соответственно)
C - соответственно)
Стороны треугольника: AB, BC, CA.
Периметр треугольника
Периметр треугольника - это сумма длин трех его сторон.
В нашем примере: 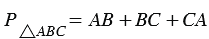 .
.
Если AB = 14 см, BC = 13 см, CA = 23 см, тогда периметр будет равен: 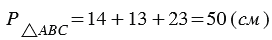 .
.
Советуем посмотреть:
Первый признак равенства треугольников
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Построения циркулем и линейкой
Правило встречается в следующих упражнениях:
7 класс
Задание 216, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 237, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 312, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 532, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 559, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 665, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 713, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1180, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 19, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1274, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник