Перпендикуляр к прямой
Возьмем прямую 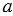 и точку А, не лежащую на этой прямой. Соединим точку А с точкой Н, лежащей на прямой
и точку А, не лежащую на этой прямой. Соединим точку А с точкой Н, лежащей на прямой 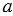 (Рис.1).
(Рис.1).
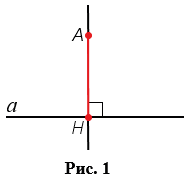
Отрезок АН называется перпендикуляром, проведенным из точки А к прямой 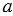 , если прямые АН и
, если прямые АН и 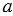 перпендикулярны.
перпендикулярны.
Теорема
| Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один. |
Доказательство:
1. Существование перпендикуляра.
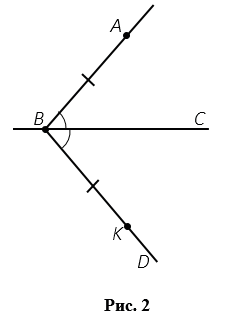
Пусть точка А не лежит на прямой ВС. Проведем луч ВА. Затем от луча ВС отложим угол СВD, равный углу АВС. На луче ВD отложим отрезок ВК, равный отрезку ВА (Рис.2).
Проведем прямую АК, пусть Н - точка пересечения прямых ВС и АК (Рис.3).
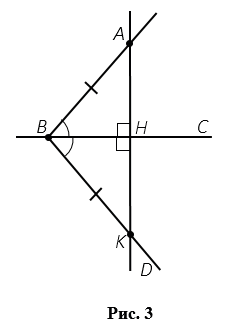
 АВН =
АВН = 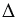 КВН по первому признаку равенства треугольников: ВН - общая сторона, ВА = ВК,
КВН по первому признаку равенства треугольников: ВН - общая сторона, ВА = ВК,  АВН =
АВН = КBН (по построению),
КBН (по построению), 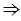
 ВНА =
ВНА = ВНD. Но
ВНD. Но  ВНА и
ВНА и  ВНD - смежные углы, тогда по свойству смежных углов
ВНD - смежные углы, тогда по свойству смежных углов  ВНА +
ВНА + ВНD = 1800, следовательно, каждый из смежных улов прямой, т.е.
ВНD = 1800, следовательно, каждый из смежных улов прямой, т.е.  ВНА =
ВНА = ВНD = 900, а значит АН
ВНD = 900, а значит АН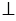 ВС.
ВС.
2. Единственность перпендикуляра.
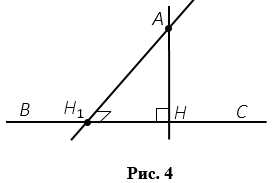
Предположим, что через точку А можно провести еще один перпендикуляр АН1 к прямой ВС, тогда получим, что две прямые АН и АН1, перпендикулярные к прямой ВС пересекаются в точке А (Рис.4). Но по свойству перпендикулярных прямых, прямые АН и АН1 пересекаться не могут, значит, наше предположение неверно и через точку А можно провести только один перпендикуляр к прямой ВС. Теорема доказана.
Проведение перпендикуляра из точки к прямой
Для проведения перпендикуляра из точки к прямой, используют чертежный угольник (Рис.5). Чертежный угольник прикладывают так, чтобы одна из его сторон, образующих прямой угол угольника, располагалась вдоль прямой, к которой нужно провести перпендикуляр. Вдоль второй стороны, образующей прямой угол угольника, проводим прямую так, чтобы она проходила через точку, из которой нужно провести перпендикуляр к прямой. Отрезок, соединяющий точку на прямой, к которой нужно провести перпендикуляр, и точку, из которой нужно провести перпендикуляр, и есть перпендикуляр проведенный из данной точки к данной прямой. На Рис.5 АН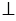
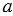 .
.
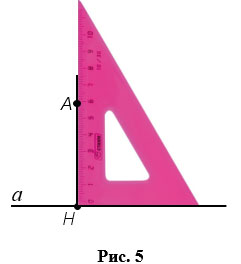
Советуем посмотреть:
Первый признак равенства треугольников
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Построения циркулем и линейкой
Правило встречается в следующих упражнениях:
7 класс
Задание 105, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 433, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 668, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1285, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник