Выпуклый многоугольник
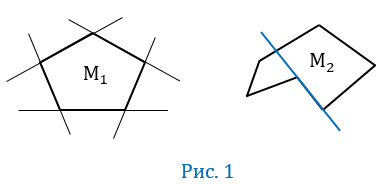
Выпуклый многоугольник - это многоугольник, который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. На рис.1 многоугольник М1 является выпуклым многоугольником, а многоугольник М2 - невыпуклым.
Сумма углов выпуклого многоугольника
Рассмотрим выпуклый 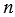 -угольник (рис.2,
-угольник (рис.2,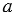 ). АnА1А2, А1А2А3, ..., Аn-1АnА1 - углы этого многоугольника. Найдем их сумму.
). АnА1А2, А1А2А3, ..., Аn-1АnА1 - углы этого многоугольника. Найдем их сумму.
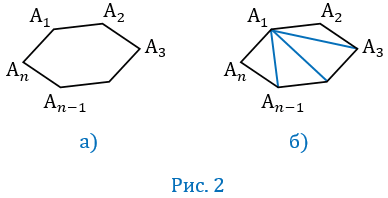
Соединим вершину А1 диагоналями с другими вершинами (рис.2, б). В итоге получим n-2 треугольника, сумма углов которых равна сумме углов n-угольника. Сумма углов каждого треугольника равна 1800, поэтому сумма углов многоугольника А1А2...Аn равна (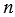 -2 )
-2 ) 1800.
1800.
Сумма углов выпуклого 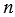 -угольника равна ( -угольника равна (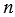 - 2) - 2) 1800. 1800. |
Примечание: Сумма углов невыпуклого 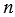 -угольника также равна (
-угольника также равна (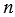 - 2)
- 2) 1800.
1800.
Внешний угол выпуклого многоугольника
Внешний угол выпуклого многоугольника - угол, смежный с углом многоугольника. На рис.3 угол OAB внешний угол многоугольника АВСDE смежный с углом ВАЕ.
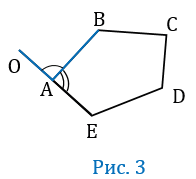
Если при каждой вершине выпуклого многоугольника А1А2...Аn взять по одному внешнему углу, то сумма этих внешних углов окажется равной
1800 - А1 + 1800 - А2 + ... + 1800 - Аn = n 1800 - (A1 + A2 + ... + An) = n
1800 - (A1 + A2 + ... + An) = n 1800 - (n-2)
1800 - (n-2) 1800 = n
1800 = n 1800 - n
1800 - n 1800 + 2
1800 + 2 1800 = 3600.
1800 = 3600.
| Сумма внешних углов выпуклого многоугольника равна 3600. |
Количество диагоналей выпуклого многоугольника
Количество диагоналей выпуклого 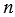 -угольника находится по формуле -угольника находится по формуле 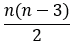 . . |
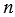 -угольника можно провести
-угольника можно провести 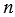 − 3 диагонали. Из всех
− 3 диагонали. Из всех 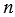 вершин можно провести
вершин можно провести 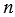 (
(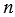 − 3) диагоналей, однако при таком подсчёте каждая диагональ учитывается дважды (объясните почему), т.е. мы нашли удвоенное число диагоналей
− 3) диагоналей, однако при таком подсчёте каждая диагональ учитывается дважды (объясните почему), т.е. мы нашли удвоенное число диагоналей 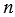 -угольника. Следовательно, число диагоналей выпуклого
-угольника. Следовательно, число диагоналей выпуклого 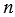 -угольника равно
-угольника равно 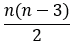 .
.Советуем посмотреть:
Симметрии фигур (осевая, центральная, поворотная, переносная)
Правило встречается в следующих упражнениях:
7 класс
Задание 364, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 365, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 424, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 724, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 812, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 813, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 860, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1079, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 464, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
9 класс