Общие касательные двух окружностей

Рассмотрим две окружности с центрами О₁ и О₂, которые касаются внутренним или внешним образом в точке касания К, лежащей на прямой О₁О₂. Тогда прямая 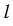, проходящая через точку К и перпендикулярная к прямой О₁О₂ (рис. 1 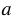, б), является касательной к каждой из окружностей, т.к. прямая проходящая через конец радиуса, лежащий на окружности, и перпендикулярная к этому радиусу, является касательной (признак касательной). В таком случае говорят, что прямая 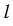является общей касательной данных окружностей.

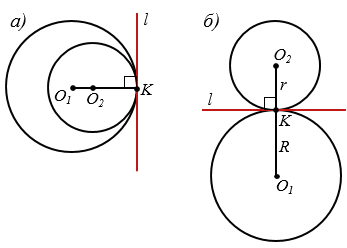
                               Рис. 1

Количество общих касательных двух окружностей

Количество общих касательных двух окружностей зависит от их взаимного расположения:

1) если все точки одной окружности являются внутренними относительно другой окружности, то такие окружности не имеют общих касательных;

2) если окружности касаются внутренним образом, то они имеют одну общую касательную (рис. 1, );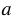

3) если две окружности пересекаются, то они имеют две общие касательные (рис. 2);

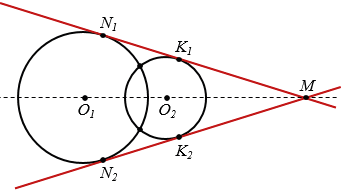
                               Рис. 2

4) если окружности касаются внешним образом, они имеют три общие касательные (рис. 3);

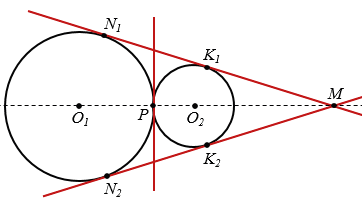
                               Рис. 3

5) если все точки каждой окружности являются внешними относительно другой окружности, то эти окружности имеют четыре общие касательные (рис. 4).

                               Рис. 4

Общую касательную к двум окружностям называют внешней, если обе окружности лежат по одну сторону от этой касательной, так на рисунке 4 прямые N₁K₁ и N₂K₂ - внешние касательные окружностей.

Общую касательную к двум окружностям называют внутренней, если обе окружности лежат по разные стороны от этой касательной, так на рисунке 4 прямые P₁T₂ и P₂T₁ - внутренние касательные окружностей.