Градусная мера дуги окружности

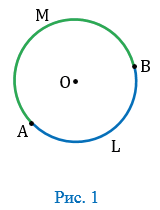
На рисунке 1 две точки А и В разделяют окружность на две дуги. На каждой дуге отмечают промежуточную точку, например L и М, для того, чтобы различать эти дуги. Обозначают дуги так: АLB  и АМВ. Если в задаче ясно, о какой из двух дуг идет речь, то используют обозначение без промежуточной точки: АВ.

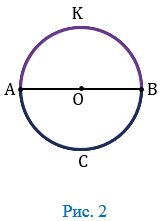
Если отрезок, соединяющий концы дуги является диаметром то, такая дуга называется полуокружностью. На рисунке 2 изображена окружность с центром О, концы диаметра АВ разделяют данную окружность на две полуокружности: АКB  и АСВ.

Центральный угол - угол с вершиной в центре окружности. Пусть стороны центрального угла окружности с центром О пересекают ее в точках А и В. Центральному углу АОВ соответствуют две дуги с концами А и В.

• Если 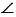АОВ развернутый, то ему соответствуют две полуокружности (Рис. 2).
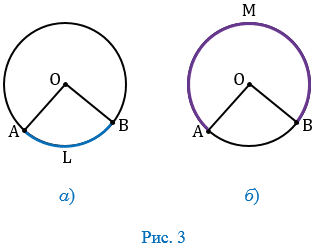
• Если 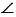АОВ неразвернутый, то дуга АLВ, расположенная внутри этого угла, меньше полуокружности (Рис. 3, $а$).
• Если АОВ неразвернутый, то дуга АМВ, расположенная во внешней области этого угла, больше полуокружности (Рис. 3, б).

Измерение дуги окружности

Дугу окружности можно измерять в градусах.

• Если дуга АВ окружности с центром О меньше полуокружности (Рис. 3, $а$) или является полуокружностью (Рис. 2), то ее градусная мера считается равной градусной мере центрального угла АОВ.
• Если дуга АВ окружности с центром О больше полуокружности (Рис. 3, б), то ее градусная мера считается равной 360⁰ - АОВ.

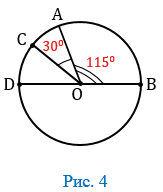
Градусная мера дуги АВ (дуги АLВ), как и сама дуга, обозначается символом АВ ( АLВ). На рисунке 4 градусная мера дуги САВ равна 145⁰. Обычно говорят кратко: "Дуга САВ равна 145⁰" и пишут: САВ = 145⁰. Также на рисунке 4 АDВ = 360⁰ - 115⁰ = 245⁰, СDВ = 360⁰ - 145⁰ = 215⁰, DВ = 180⁰.