Ромб и квадрат
Частным видом параллелограмма является ромб.
| Ромбом называется параллелограмм, у которого все стороны равны |
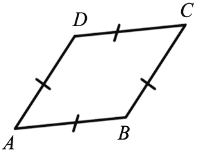
ABCD - ромб.
Ромб обладает всеми свойствами параллелограмма.
Особое свойство ромба
| Диагонали ромба взаимно перпендикулярны и делят его углы пополам |
Доказательство
Дано: ABCD - ромб
Доказать: AC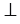 BD,
BD,  ADO =
ADO =  CDO
CDO
Доказательство:
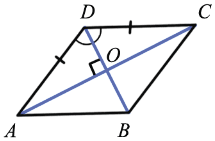
AD = DC (по определению ромба), значит,  ADC - равнобедренный.
ADC - равнобедренный.
AO = OC (по свойству диагоналей параллелограмма),  DO - медиана
DO - медиана  ADC , а в равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой,
ADC , а в равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой,  AC
AC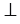 BD,
BD,  ADO =
ADO =  CDO, что и требовалось доказать.
CDO, что и требовалось доказать.
Теорема
| Если диагонали параллелограмма перпендикулярны, то этот параллелограмм - ромб (признак ромба) |
Доказательство
Дано: ABCD - параллелограмм, AC BD
BD
Доказать: ABCD - ромб
Доказательство:
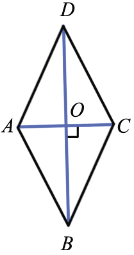
Рассмотрим  AOВ и
AOВ и  COВ:
COВ:
Т.к. AC BD, то
BD, то AOВ =
AOВ =  COВ = 900;
COВ = 900;
AO = OC (по свойству диагоналей параллелограмма), ОВ - общий катет, 
 AOВ =
AOВ =  COВ (по двум катетам). В равных треугольниках против соответственно равных углов лежат равные стороны,
COВ (по двум катетам). В равных треугольниках против соответственно равных углов лежат равные стороны,  ВС = ВА.
ВС = ВА.
В параллелограмме противоположные стороны равны,  AD = BC, AB = DC
AD = BC, AB = DC
Итак: ABCD - параллелограмм (по условию) AD = BC = AB = DC (по доказанному).  ABCD - ромб, что и требовалось доказать.
ABCD - ромб, что и требовалось доказать.
Теорема
| Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм - ромб (признак ромба) |
Доказательство
Дано: ABCD - параллелограмм, АС - диагональ и биссектриса  DAB и
DAB и DCB
DCB
Доказать: ABCD - ромб
Доказательство:
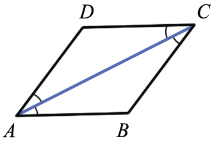
 DAB =
DAB = DCB (по свойству параллелограмма), а АС -биссектриса
DCB (по свойству параллелограмма), а АС -биссектриса  DAB и
DAB и DCB (т.е. АС делит эти углы на два равных угла),
DCB (т.е. АС делит эти углы на два равных угла), 
 DAC =
DAC =  BAC =
BAC = DCA =
DCA =  BCA
BCA
Рассмотрим  ADC:
ADC:  DAC =
DAC = DCA,
DCA, 
 ADC - равнобедренный с основанием AC, и AD = DC. В параллелограмме противоположные стороны равны,
ADC - равнобедренный с основанием AC, и AD = DC. В параллелограмме противоположные стороны равны,  AD = BC, AB = DC
AD = BC, AB = DC
Итак: ABCD - параллелограмм (по условию) AD = BC = AB = DC (по доказанному).  ABCD - ромб, что и требовалось доказать.
ABCD - ромб, что и требовалось доказать.
Две теоремы, доказанные выше, называют признаками ромба.
| Квадратом называется прямоугольник, у которого все стороны равны |
Основные свойства квадрата:
1. Все углы квадрата прямые.
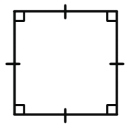
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
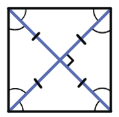
Признаки квадрата:
- Если две смежные стороны прямоугольника равны, то этот прямоугольник является квадратом.
- Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом.
- Если один из углов ромба прямой, то этот ромб является параллелограммом.
- Если диагонали ромба равны, то этот ромб является квадратом.
Советуем посмотреть:
Симметрии фигур (осевая, центральная, поворотная, переносная)
Правило встречается в следующих упражнениях:
7 класс
Задание 412, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 467, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 728, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 851, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 997, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1169, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1178, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1237, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1269, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1287, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Упражнение 903, Макарычев, Миндюк, Нешков, Суворова, Учебник