Теорема о вписанном угле
Вписанный угол - угол, вершина которого лежит на окружности, а стороны пересекают окружность.
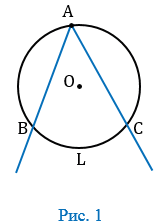
На рисунке 1 угол ВАС вписанный, дуга ВLС расположена внутри этого угла. В таком случае говорят, что вписанный угол АВС опирается на дугу ВLC.
Теорема
| Вписанный угол измеряется половиной дуги, на которую он опирается. |
Доказательство
Дано: окружность (О),  АВС - вписанный,
АВС - вписанный,  АС - внутри
АС - внутри  АВС.
АВС.
Доказать:  АВС =
АВС = 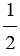
 АС.
АС.
Доказательство:
1 случай
Луч ВО совпадает с одной из сторон угла АВС.
Пусть ВО совпадает с ВС (Рис. 2).
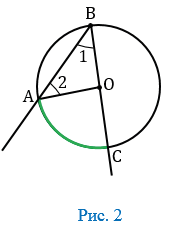
В данном случае дуга АС меньше полуокружности, следовательно,  АОС =
АОС = АС (т.к.
АС (т.к.  АОС - центральный угол, причем он меньше полуокружности, поэтому градусная мера центрального угла равна градусной мере дуги, на которую он опирается).
АОС - центральный угол, причем он меньше полуокружности, поэтому градусная мера центрального угла равна градусной мере дуги, на которую он опирается).
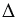 АВО - равнобедренный с основанием АВ (т.к. ОА = ОВ - радиусы),
АВО - равнобедренный с основанием АВ (т.к. ОА = ОВ - радиусы), 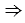
 1 =
1 =  2 (углы при основании).
2 (углы при основании).  АОС - внешний угол
АОС - внешний угол 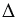 АВО,
АВО, 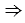
 АОС =
АОС =  1 +
1 +  2 = 2
2 = 2 1. Следовательно, учитывая то, что
1. Следовательно, учитывая то, что  АОС =
АОС = АС, получим:
АС, получим:  АС = 2
АС = 2  1, откуда
1, откуда  1 =
1 = 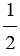
 АС, т.е.
АС, т.е.  АВС =
АВС = 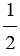
 АС.
АС.
2 случай
Луч ВО делит угол АВС на два угла.
В данном случае луч ВО пересекает дугу АС в некоторой точке D (Рис. 3).
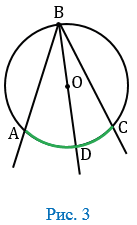
Точка D разделят дугу АС на две дуги:  АD и
АD и  DС, поэтому
DС, поэтому  АС =
АС =  АD +
АD +  DС.
DС.
Луч ВD разделяет угол АВС на два угла, поэтому  АВС =
АВС =  АВD +
АВD +  DВС.
DВС.
По доказанному в 1 случае  АВD =
АВD = 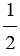
 АD и
АD и  DВС =
DВС = 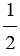
 DС. Складывая эти равенства, получаем:
DС. Складывая эти равенства, получаем:  АВD +
АВD +  DВС =
DВС = 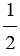
 АD +
АD + 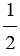
 DС или
DС или  АВD +
АВD +  DВС =
DВС = 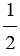 (
( АD +
АD +  DС). Следовательно,
DС). Следовательно,  АВС =
АВС = 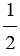
 АС.
АС.
3 случай
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла.
В данном случае луч ВС пересекает дугу АD в точке С (Рис. 4).
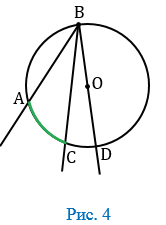
Точка С разделят дугу АD на две дуги:  АC и
АC и  CD, поэтому
CD, поэтому  АD =
АD =  АC +
АC +  CD, откуда
CD, откуда  АC =
АC =  АD -
АD -  CD.
CD.
Луч ВС разделяет угол АВD на два угла, поэтому  АВD =
АВD =  АВC +
АВC +  CВD, откуда
CВD, откуда  АВC =
АВC =  АВD -
АВD -  CВD.
CВD.
По доказанному в 1 случае  АВD =
АВD = 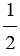
 АD и
АD и  СВD =
СВD = 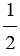
 СD. Вычитая из первого равенства второе, получаем:
СD. Вычитая из первого равенства второе, получаем:  АВD -
АВD -  СВD =
СВD = 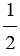
 АD -
АD - 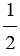
 CD или
CD или  АВD -
АВD -  СВD =
СВD = 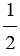 (
( АD -
АD -  CD). Следовательно,
CD). Следовательно,  АВС =
АВС = 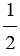
 АС.
АС.
Теорема доказана.
Следствия из теоремы о вписанном угле
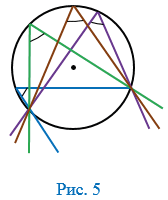
| 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (Рис. 5). |
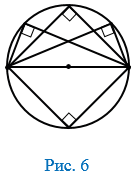
| 2. Вписанный угол, опирающийся на полуокружность, - прямой (рис. 6). |
Теорема
| Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. |
Доказательство
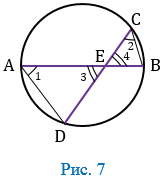
Дано: окружность, АВ и СD - хорды, АВ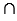 СD = Е (Рис. 7).
СD = Е (Рис. 7).
Доказать: АЕ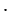 ВЕ = СЕ
ВЕ = СЕ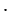 DЕ.
DЕ.
Доказательство:
В 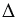 АDЕ и
АDЕ и 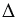 СВЕ:
СВЕ:  1 =
1 =  2, т.к. они вписанные и опираются на одну и ту же дугу ВD (смотри следствие 1 из теоремы о вписанном угле),
2, т.к. они вписанные и опираются на одну и ту же дугу ВD (смотри следствие 1 из теоремы о вписанном угле),  3 =
3 =  4 как вертикальные углы, следовательно, треугольники АDЕ и СВЕ подобны (по 1 признаку подобия треугольников). В подобных треугольниках сходственные стороны пропорциональны, поэтому
4 как вертикальные углы, следовательно, треугольники АDЕ и СВЕ подобны (по 1 признаку подобия треугольников). В подобных треугольниках сходственные стороны пропорциональны, поэтому 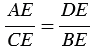 , откуда АЕ
, откуда АЕ ВЕ = СЕ
ВЕ = СЕ DЕ. Теорема доказана.
DЕ. Теорема доказана.
Теорема
| Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой. |
Доказательство
Дано: окр.(О, 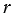 ), АВ - хорда, АС - касательная, А - точка касания.
), АВ - хорда, АС - касательная, А - точка касания.
Доказать:  ВАС =
ВАС = 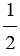
 АВ.
АВ.
Доказательство:
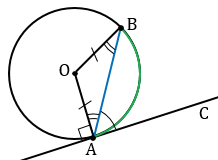
 АОВ - равнобедренный с основанием АВ, т.к. ОА = ОВ =
АОВ - равнобедренный с основанием АВ, т.к. ОА = ОВ = 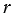 , значит,
, значит,  ОАВ =
ОАВ =  ОВА (как углы при основании), при этом ОА
ОВА (как углы при основании), при этом ОА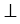 АС (свойство касательной), поэтому
АС (свойство касательной), поэтому  ОАВ =
ОАВ =  ОВА = 900 -
ОВА = 900 -  ВАС. Следовательно, по теореме о сумме углов треугольника:
ВАС. Следовательно, по теореме о сумме углов треугольника:  АОВ = 1800 - 2(900 -
АОВ = 1800 - 2(900 -  ВАС) = 1800 - 1800 + 2
ВАС) = 1800 - 1800 + 2 ВАС = 2
ВАС = 2 ВАС, откуда
ВАС, откуда  ВАС =
ВАС = 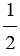
 АОВ.
АОВ.  АОВ - центральный, поэтому
АОВ - центральный, поэтому  ВАС =
ВАС = 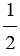
 АВ. Теорема доказана.
АВ. Теорема доказана.
Советуем посмотреть:
Свойства диаметров и хорд окружности
Взаимное расположение прямой и окружности
Взаимное расположение двух окружностей
Общие касательные двух окружностей
Градусная мера дуги окружности
Углы, образованные хордами, касательными и секущими
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 657, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 658, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 667, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 705, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 732, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 887, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 889, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 890, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 14, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 802, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник