Высоты треугольника
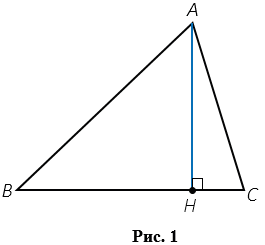
Высота треугольника - это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. На Рис.1 АН - высота треугольника АВС (точку Н называют основанием высоты АН).
Любой треугольник имеет три высоты. На Рис.2 (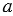 ), АН, ВМ, СК - высоты треугольника АВС (АН
), АН, ВМ, СК - высоты треугольника АВС (АН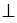 ВС, ВМ
ВС, ВМ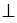 АС, СК
АС, СК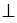 АВ).
АВ).
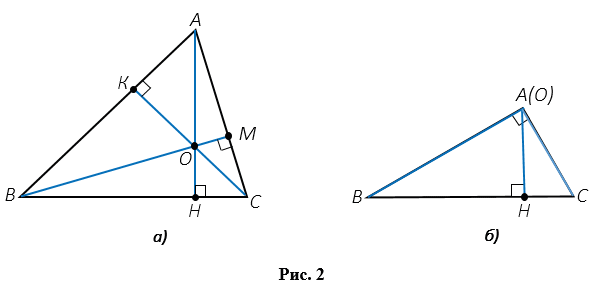
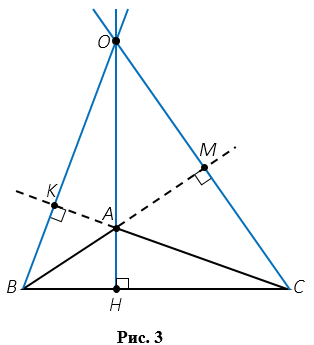
Замечательное свойство высот треугольника: в любом треугольнике высоты или их продолжения пересекаются в одной точке. На Рис.2 ( 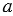 ,б ) в точке О пересекаются высоты треугольника АВС, а на Рис.3 в точке О пересекаются продолжения высот треугольника АВС.
,б ) в точке О пересекаются высоты треугольника АВС, а на Рис.3 в точке О пересекаются продолжения высот треугольника АВС.
Советуем посмотреть:
Первый признак равенства треугольников
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Построения циркулем и линейкой
Правило встречается в следующих упражнениях:
7 класс
Задание 264, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 272, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 347, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 487, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 499, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 607, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1251, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 459, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 793, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
9 класс