Квадратичная функция и её график / Функции / Алгебра / Справочник по математике 5-9 класс

Определение

Квадратичной функцией называется функция, которую можно задать формулой вида

\(y=ax^2+bx+c,\)

где \(x\) - независимая переменная, \(a, b\) и \(c\) - некоторые числа, причём \(a\ne0.\)

Область определения данной функции: \(D(f)=(-\infty; +\infty).\)

I. Функция \(y=ax^2\), ее график и свойства.

График функции \(y=ax^2\), где \(a\ne0\), как и график функции \(y=x^2,\) называется параболой.

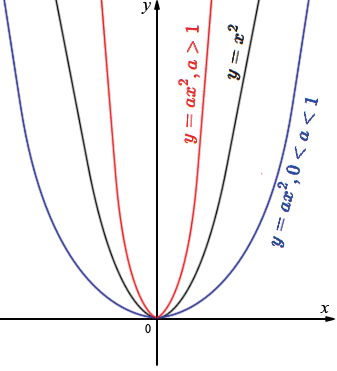
Графиком функции \(y=ax^2\) является парабола, которая получается из параболы \(y=x^2\) растяжением от оси \(x\) в \(a\) раз, если \(a>1\), и сжатием к оси \(x\) в \(\frac1a\) раза, если \(0\lt a\lt 1\)

Графики функций \(y=ax^2\) и \(y=-ax^2\) (при \(a\ne0\)) симметричны относительно оси \(x\). На рисунке представлены графики для случая \(a>0.\)

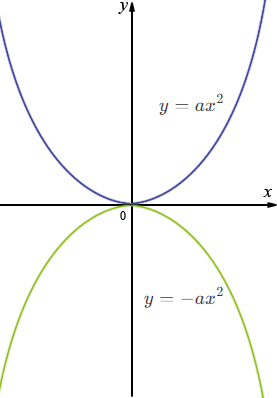
Свойства функции \(y=ax^2\) при \(a>0.\)

Область определения функции - множество всех чисел, т.е. \(D(y)=(-\infty; +\infty).\)
Если \(x=0\), то \(y=0\). График функции проходит через начало координат.
Если \( x\ne0 \), то \(y>0\). График функции расположен в верхней полуплоскости.
Противоположным значениям аргумента соответствуют равные значения функции; график функции симметричен относительно оси \(y.\) Функция является четной.
Функция убывает на промежутке \( (-\infty; 0]\) и возрастает на промежутке \([0; +\infty)\).
Наименьшее значение, равное нулю, функция принимает при \(x=0\), наибольшего значения функция не имеет.
Множество значений функции - множество неотрицательных чисел, т.е. \(E(y)=[0; +\infty)\).

Свойства функции \(y=ax^2\) при \(a<0.\)

Область определения функции - множество всех чисел, т.е. \(D(y)=(-\infty; +\infty).\)
Если \(x=0\), то \(y=0\). График функции проходит через начало координат.
Если \( x\ne0 \), то \(y<0\). График функции расположен в нижней полуплоскости.
Противоположным значениям аргумента соответствуют равные значения функции; график функции симметричен относительно оси \(y.\) Функция является четной.
Функция возрастает на промежутке \( (-\infty; 0]\) и убывает на промежутке \([0; +\infty)\).
Наибольшее значение, равное нулю, функция принимает при \(x=0\), наименьшего значения функция не имеет.
Множество значений функции - множество неположительных чисел, т.е. \(E(y)=(-\infty; 0]\).

Следовательно:

при \(a>0\) ветви параболы \(y=ax^2\) направлены вверх;
при \(a<0\) ветви параболы \(y=ax^2\) направлены вниз.

Точку пересечения параболы с ее осью симметрии называют вершиной параболы.

II. Графики функций \(y=ax^2+n\) и \(y=a(x-m)^2\).

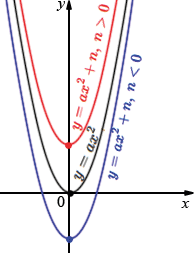
График функции \(y=ax^2+n\) является параболой, которую можно получить из графика функции \(y=ax^2\) с помощью параллельного переноса вдоль оси \(y\) на \(n\) единиц вверх, если \(n>0,\) или на \(-n\) единиц вниз, если \(n<0.\)

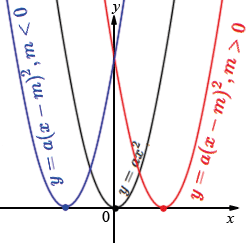
График функции \(y=a(x-m)^2\) является параболой, которую можно получить из графика функции \(y=ax^2\) с помощью параллельного переноса вдоль оси \(x\) на \(m\) единиц вправо, если \(m>0\), или на \(-m\) единиц влево, если \(m<0\).

График функции \(y=a(x-m)^2+n\) является параболой, которую можно получить из графика функции функции \(y=ax^2\) с помощью двух параллельных переносов: сдвига вдоль оси \(x\) на \(m\) единиц вправо, если \(m>0\), или на \(-m\) единиц влево, если \(m<0\), и сдвига вдоль оси \(y\) на на \(n\) единиц вверх, если \(n>0,\) или на \(-n\) единиц вниз, если \(n<0.\)

Заметим, что параллельные переносы можно производить в любом порядке: сначала выполнить параллельный перенос вдоль оси \(x\), а затем - вдоль оси \(y\) или наоборот.

III. Построение графика квадратичной функции.

Графиком функции \(y=ax^2+bx+c\) является парабола, которую можно получить из графика функции \(y=ax^2\) с помощью двух параллельных переносов - сдвига вдоль оси \(x\) и сдвига вдоль оси \(y.\) Вершиной данной параболы является точка \((m; n),\) где \(m=-\frac{b}{2a}\), \(n=-\frac{b^2-4ac}{4a.}\) Заметим, что ординату \(n\) можно находить, подставив найденное значение абсциссы в формулу \(y=ax^2+bx+c\). Осью симметрии параболы является прямая \(x=m,\) параллельная оси \(y.\) При \(a>0\) ветви параболы направленны вверх, а при \(a<0\) - вниз.

Чтобы построить график квадратичной функции, нужно:

1) Определить направление ветвей параболы.

2) Найти координаты вершины параболы и отметить ее в координатной плоскости. Определить ось симметрии параболы.

3) Найти нули функции.

4) Найти точку пересечения с осью \(Oy\).

5) Построить еще несколько точек, принадлежащих параболе.

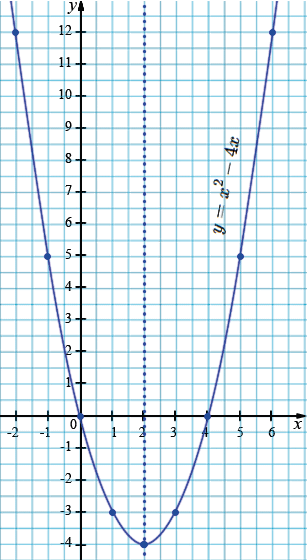
Например, построим график функции \( y=x^2 - 4x\).

1. Графиком данной функции является парабола, ветви которой направлены вверх \((a=1>0).\)

2. \(m = -\frac{b}{2a} = \frac{4}{2} = 2 \)

\(n = 2^2 - 4\cdot 2 = 4 - 8 = -4. \)

Вершина параболы: \((2; -4)\). Прямая \(x=2\) - ось симметрии параболы.

3. Нули функция: