Одночлены
Определение:
| Одночлены - это выражения, представляющие собой произведение чисел, переменных и их степеней. |
Все числа, любые переменные и их степени также принято считать одночленами.
Примеры одночленов:
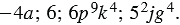
Если одночлен представлен в виде произведения числового множителя, который стоит на первом месте, и степеней с различными основаниями, то его называют одночленом стандартного вида.
Например, упростим одночлен 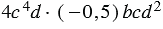 :
:
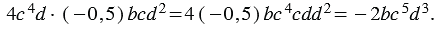
То есть 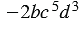 - это стандартный вид одночлена
- это стандартный вид одночлена 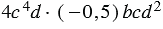 .
.
Примеры одночленов стандартного вида:
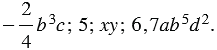
Нуль-одночленами называют число 0 и одночлены, которые тождественно равны нулю (например 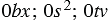 и т.п.). Нуль-одночлены не относят к одночленам стандартного вида.
и т.п.). Нуль-одночлены не относят к одночленам стандартного вида.
Определение:
| Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена. |
Например, коэффициент одночлена 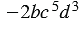 равен
равен 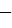 2. При этом любой одночлен стандартного вида имеет коэффициент, даже если при их записи числовой множитель не используется. Примером таких одночленов может быть
2. При этом любой одночлен стандартного вида имеет коэффициент, даже если при их записи числовой множитель не используется. Примером таких одночленов может быть 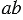 и
и 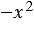 , их коэффициенты соответственно равны 1 и
, их коэффициенты соответственно равны 1 и 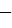 1, так как очевидно, что
1, так как очевидно, что 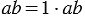 и
и 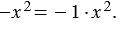
Одночлены, у которых одинаковые буквенные части, называют подобными. Например, подобны будут одночлены 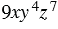 и
и 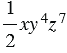 . Числа также относятся к подобным одночленам, то есть, например, одночлены
. Числа также относятся к подобным одночленам, то есть, например, одночлены 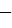 6 и 102 - подобны.
6 и 102 - подобны.
Определение:
| Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, который является числом, отличным от нуля, считают равной нулю. |
Например:
Степень одночлена 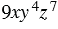 равна 12; степень одночлена
равна 12; степень одночлена 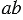 равна 2; степень одночлена
равна 2; степень одночлена 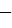 7 равна 0.
7 равна 0.
При этом считают, что нуль-одночлен степени не имеет.
Мы можем умножать и возводить в степень одночлены, при этом результатом будет также одночлен, который необходимо представить в стандартном виде. При умножении одночленов и возведении одночлена в степень используют правило умножения степеней с одинаковыми основаниями и правило возведения степени в степень.
Например, пусть нам даны одночлены 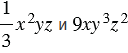 , тогда одночлен
, тогда одночлен 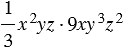 будет являться их произведением. Упростим его и представим в стандартном виде, используя переместительное и сочетательное свойство умножения:
будет являться их произведением. Упростим его и представим в стандартном виде, используя переместительное и сочетательное свойство умножения:
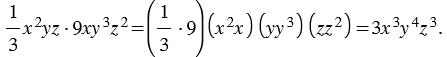
Например, возведем в куб одночлен 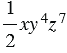 и приведем полученный одночлен к стандартному виду:
и приведем полученный одночлен к стандартному виду:
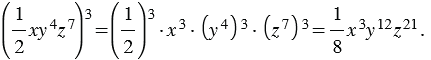
Советуем посмотреть:
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
7 класс
Номер 420, Мерзляк, Полонский, Якир, Учебник
Номер 458, Мерзляк, Полонский, Якир, Учебник
Номер 488, Мерзляк, Полонский, Якир, Учебник
Номер 542, Мерзляк, Полонский, Якир, Учебник
Номер 612, Мерзляк, Полонский, Якир, Учебник
Номер 817, Мерзляк, Полонский, Якир, Учебник
Номер 1201, Мерзляк, Полонский, Якир, Учебник
Номер 8, Мерзляк, Полонский, Якир, Учебник
Упражнение 478, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 633, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 5, Мерзляк, Полонский, Якир, Учебник
Номер 42, Мерзляк, Полонский, Якир, Учебник
Номер 61, Мерзляк, Полонский, Якир, Учебник
Номер 109, Мерзляк, Полонский, Якир, Учебник
Номер 115, Мерзляк, Полонский, Якир, Учебник
Номер 132, Мерзляк, Полонский, Якир, Учебник
Номер 9, Мерзляк, Полонский, Якир, Учебник
Номер 268, Мерзляк, Полонский, Якир, Учебник
Номер 467, Мерзляк, Полонский, Якир, Учебник
Номер 868, Мерзляк, Полонский, Якир, Учебник
9 класс