Функция у=х^2 и ее график

Рассмотрим функцию, которая связывает координаты следующим соотношением: .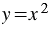

Чтобы построить график рассматриваемой функции, определим несколько значений этой функции 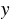для некоторых значений аргумента .

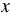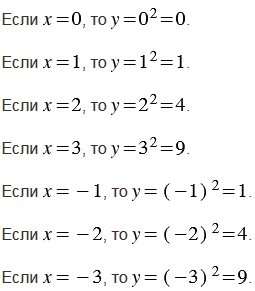
Составим таблицу значений функции 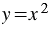для указанных выше значений аргумента .

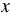Теперь отмечаем в прямоугольной системе координат точки с координатами (0; 0), (1; 1), (2; 4),  (3; 9), 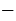 (1; 1),  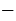(2; 4), (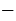3; 9).

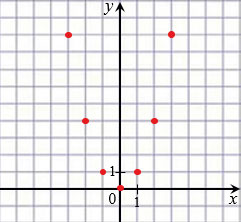
Далее соединяем отмеченные точки плавной линией.

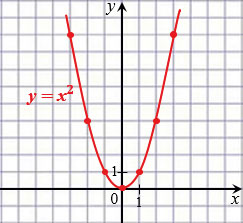
Мы построили график функции 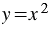и этот график называют параболой.

Можно вычислить координаты других точек, удовлетворяющих равенству 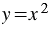, и отметить их на координатной плоскости. Все они попадут на эту параболу.

Точка с координатами (0; 0) делит параболу на две равные части, называемые ветвями параболы, эти ветви неограниченно уходят вверх. Саму точку с координатами (0; 0), называют вершиной параболы. В вершине одна ветвь параболы плавно переходит в другую.

Свойства функции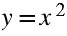

1. Областью определения функции 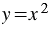являются все числа.
2. Областью значений функции 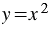являются все неотрицательные числа, так квадрат любого числа положителен или равен нулю, то есть при любом 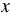выполняется неравенство .
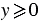3. Если 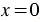, то 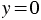. Поэтому график функции 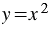проходит через начало координат. Также, запомните, значение аргумента, при котором значение функции равно нулю, называют нуль функции. Значит, 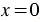- нуль функции .
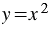4. Если , то 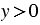 . Значит, все точки графика функции, кроме точки (0; 0), расположены выше оси  .
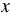5. Противоположным значениям 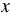соответствует одно и то же значение 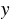. Это следует из того, что 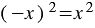при любом 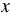. Значит, точки графика функции 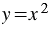, имеющие противоположные абсциссы, симметричны относительно оси 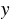, поэтому ось ординат является осью симметрии параболы. Также функцию симметричную относительно оси ординат называют четной функцией, значит, функция 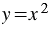является четной.