Линейная функция, ее график и свойства
Определение:
Функцию, которую можно задать формулой вида 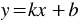 , , 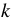 и и 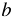 - некоторые числа, - некоторые числа, 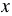 - независимая переменная, называют линейной. - независимая переменная, называют линейной. |
Примеры линейных функций:
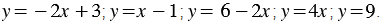
Областью определения линейной функции являются все числа.
Графиком линейной функции является прямая.
Построим график функции 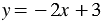 .
.
Составим таблицу значений этой функции 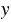 для некоторых значений аргумента
для некоторых значений аргумента 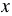 .
.
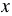 |
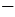 3 3 |
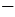 2 2 |
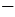 1 1 |
0 | 1 | 2 | 3 |
 |
9 | 7 | 5 | 3 | 1 |  1 1 |
 3 3 |
Отметим точки с координатами ( 3; 9), (
3; 9), (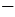 2; 7), (
2; 7), (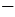 1; 5), (0; 3), (1; 1), (2;
1; 5), (0; 3), (1; 1), (2; 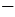 1), (3;
1), (3; 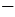 3) на координатной плоскости.
3) на координатной плоскости.
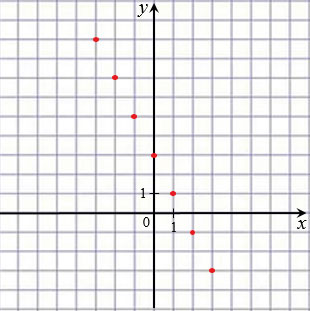
Все точки, отмеченные на координатной плоскости, лежат на одной прямой, которая и является графиком функции 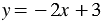 .
.
Вспомним, фигура может быть графиком некоторой функции, если любая прямая, перпендикулярная оси абсцисс, имеет с этой фигурой не более одной точки. Следовательно, прямая, которая является графиком линейной функции, не может быть вертикальной.
Прямая однозначно задается любыми двумя точками, поэтому для построения графика линейной функции достаточно выбрать два произвольных значения аргумента и составить таблицу значений функции, имеющую лишь два столбца.
Пример. Постройте график функции 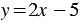 .
.
Решение: Составим таблицу значений этой функции 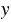 для некоторых значений аргумента
для некоторых значений аргумента 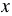 .
.
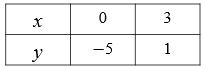
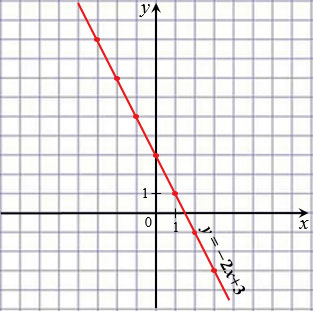
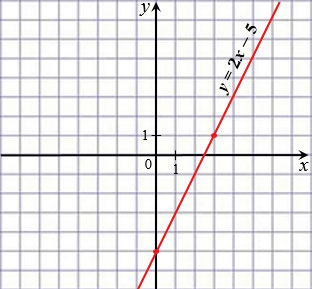
Отметим на координатной плоскости точки с координатами (0; 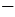 5) и (3; 1) и проведем через них прямую, которая является графиком линейной функции
5) и (3; 1) и проведем через них прямую, которая является графиком линейной функции 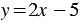 .
.
Частные случаи линейной функции:
1) Если 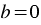 и
и 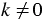 , то
, то 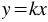 .
.
Функцию 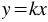 называют прямой пропорциональностью.
называют прямой пропорциональностью.
Примеры прямых пропорциональностей:
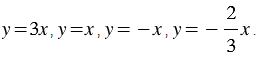
Графиком функции прямой пропорциональности является прямая, которая проходит через точку О(0; 0), т.к. если 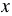 = 0, то при любом значении
= 0, то при любом значении 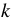 получаем
получаем 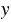 = 0. Поэтому для построения графика прямой пропорциональности достаточно указать какую-нибудь точку графика, отличную от начала координат, и провести прямую через эту точку и точку О(0; 0).
= 0. Поэтому для построения графика прямой пропорциональности достаточно указать какую-нибудь точку графика, отличную от начала координат, и провести прямую через эту точку и точку О(0; 0).
На рисунке ниже изображены графики прямых пропорциональностей, указанных выше.
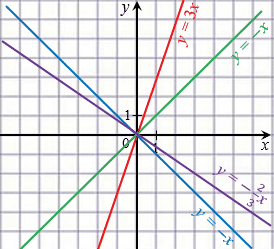
2) Если 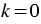 , то
, то 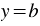 .
.
Значения функции 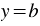 остаются неизменными при любых изменениях значений аргумента.
остаются неизменными при любых изменениях значений аргумента.
Графиком функции 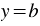 , где
, где 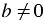 является прямая, параллельная оси
является прямая, параллельная оси 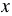 , т.к. ордината (координата
, т.к. ордината (координата 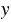 ) для любого значения
) для любого значения 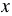 будет иметь одно и то же значение
будет иметь одно и то же значение 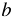 . Если же
. Если же 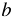 = 0, то
= 0, то 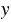 = 0 и графиком этой функции является ось абсцисс.
= 0 и графиком этой функции является ось абсцисс.
На рисунке ниже изображены графики функций 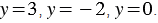
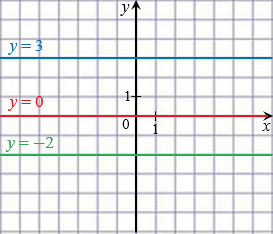
Свойства линейной функции
1. Функция определена при любых значениях переменной \(x\), т.е. \(D(y) = R\).
2. Значение функции может быть любое число, т.е. \(E(y) = R\).
3. Функция обращается в нуль при \(x = -\frac{b}{k}\).
Это свойство вытекает из решения уравнения \(kx + b = 0\), откуда получаем \(kx = -b\), тогда \(x = -\frac{b}{k}\).
4. При \(k > 0\) функция принимает отрицательные значения на промежутке \((-\infty; -\frac{b}{k})\) и положительные значения на промежутке \((-\frac{b}{k}; +\infty)\).
Это свойство вытекает из решения неравенств:
\(kx + b < 0\) и \(kx + b > 0\).
Решив указанные неравенства, найдем, что если \(k > 0\), то \(y < 0\) при \(x < -\frac{b}{k}\) и \(y > 0\) при \(x > -\frac{b}{k}\).
При \(k < 0\) функция принимает отрицательные значения на промежутке \((-\frac{b}{k}; +\infty)\) и положительные значения на промежутке \((-\infty; -\frac{b}{k})\).
Это свойство вытекает из решения неравенств:
\(kx + b < 0\) и \(kx + b > 0\), учитывая то, что \(k < 0\) (то есть не забываем, что при делении неравенства на отрицательное число, знак неравенства меняется).
5. При \(k>0\) функция \(y = kx + b\) является возрастающей, а при \(k < 0\) - убывающей.
Советуем посмотреть:
Связи между величинами. Функция, ее свойства
Функции y=x^-1 и y= x^-2 и их свойства
Квадратичная функция и её график
Дробно-линейная функция и ее график
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
7 класс
Номер 885, Мерзляк, Полонский, Якир, Учебник
Номер 892, Мерзляк, Полонский, Якир, Учебник
Номер 1010, Мерзляк, Полонский, Якир, Учебник
Упражнение 305, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 318, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 321, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 337, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 366, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 370, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 416, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 12, Мерзляк, Полонский, Якир, Учебник
Номер 310, Мерзляк, Полонский, Якир, Учебник
Номер 358, Мерзляк, Полонский, Якир, Учебник
Упражнение 398, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 546, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 556, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 642, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 675, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1171, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1316, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс