Линейное уравнение с одной переменной
Нам известно, что решить уравнение - значит найти все его корни или показать, что их нет вообще. Также нам известно, что при решении уравнений используют следующие свойства:
- корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак;
- корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.
|
Уравнение вида |
Примеры линейных уравнений с одной переменной:
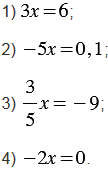
Выясним, сколько корней может иметь линейное уравнение 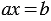 .
.
1) Если в линейном уравнении 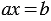 коэффициент
коэффициент 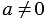 , то разделив обе части этого уравнения на
, то разделив обе части этого уравнения на 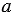 , получим
, получим 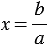 . Значит, линейное уравнение
. Значит, линейное уравнение 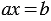 , в котором
, в котором 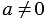 , имеет единственный корень, равный
, имеет единственный корень, равный 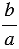 .
.
2) Если в линейном уравнении 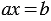 коэффициент
коэффициент 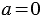 и
и 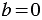 , то получим уравнение
, то получим уравнение 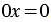 . Значит, линейное уравнение
. Значит, линейное уравнение 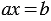 , в котором
, в котором 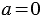 и
и 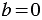 , имеет бесконечного много корней, т.е. его корнем является любое число (т.к. при умножении любого числа на ноль всегда получится ноль).
, имеет бесконечного много корней, т.е. его корнем является любое число (т.к. при умножении любого числа на ноль всегда получится ноль).
3) Если в линейном уравнении 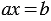 коэффициент
коэффициент 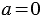 и
и 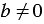 , то при любом значении
, то при любом значении 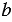 получим неверное равенство
получим неверное равенство 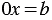 . Значит, линейное уравнение
. Значит, линейное уравнение 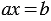 , в котором
, в котором 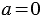 и
и 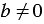 , не имеет корней.
, не имеет корней.
Вывод:
Значения 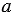 и и 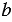 |
Корни уравнения 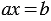 |
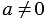 |
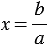 |
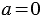 и и 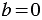 |
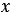 - любое число - любое число |
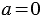 и и 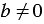 |
корней нет |
Решение многих уравнений сводится к решению линейных уравнений.
Пример:
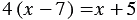 .
.
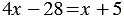 .
.
Перенесем слагаемое 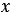 в левую часть уравнения, а слагаемое
в левую часть уравнения, а слагаемое 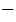 28 в правую часть, изменив при этом их знаки:
28 в правую часть, изменив при этом их знаки:
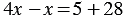 .
.
Приведем подобные слагаемые:
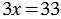 .
.
Разделим обе части уравнения на 3:
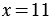 .
.
При решении исходного уравнения мы применяли свойства уравнений и выполняли тождественные преобразования, последовательно заменяя одно уравнение другим, равносильным ему. Значит, корнем уравнения 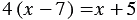 является число 11.
является число 11.
В рассматриваемом примере исходное уравнение 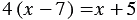 свелось к равносильному линейному уравнению
свелось к равносильному линейному уравнению 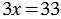 , в котором коэффициент при переменной отличен от нуля (
, в котором коэффициент при переменной отличен от нуля (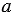 = 3).
= 3).
Если при решении уравнения равносильное ему линейное уравнение получится вида 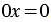 , то исходное уравнение имеет бесконечно много корней.
, то исходное уравнение имеет бесконечно много корней.
Если при решении уравнения равносильное ему линейное уравнение получится вида 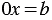 , то исходное уравнение не имеет корней.
, то исходное уравнение не имеет корней.
Советуем посмотреть:
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
7 класс
Номер 585, Мерзляк, Полонский, Якир, Учебник
Номер 1038, Мерзляк, Полонский, Якир, Учебник
Номер 1055, Мерзляк, Полонский, Якир, Учебник
Номер 1091, Мерзляк, Полонский, Якир, Учебник
Номер 1113, Мерзляк, Полонский, Якир, Учебник
Упражнение 772, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 942, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1070, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1188, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1215, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 198, Мерзляк, Полонский, Якир, Учебник
Номер 213, Мерзляк, Полонский, Якир, Учебник
Номер 266, Мерзляк, Полонский, Якир, Учебник
Номер 649, Мерзляк, Полонский, Якир, Учебник
Упражнение 216, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 631, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 636, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 722, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 723, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1045, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс