Свойства степени с натуральным показателем
Основное свойство степени
Для любого числа 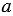 и любых натуральных чисел и любых натуральных чисел 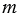 и и 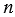 справедливо равенство: справедливо равенство: 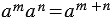 . . |
Тождество 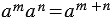 выражает основное свойство степени.
выражает основное свойство степени.
Основное свойство степени распространяется и на произведение трех и более степеней: 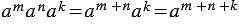 .
.
Из основного свойства степеней получаем правило умножения степеней:
| при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают. |
Примеры:
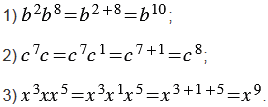
Частное степеней
Для любого числа 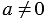 и любых натуральных чисел и любых натуральных чисел 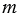 и и 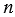 , таких, что , таких, что 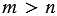 , справедливо равенство: , справедливо равенство: 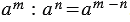 . . |
Правило деления степеней:
| при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. |
Примеры:
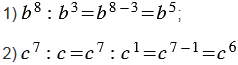
Если правило деления применить к частному 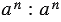 (т.е. когда
(т.е. когда 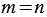 ), то получится
), то получится
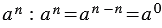 .
.
Степень с нулевым показателем не была определена, но при всяком 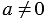 и любом натуральном
и любом натуральном 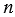 справедливо равенство:
справедливо равенство:
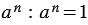 .
.
Получается, можно считать, что при 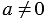 , справедливо равенство:
, справедливо равенство:
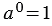 .
.
Степень числа 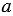 , не равного нулю, с нулевым показателем равна единице. , не равного нулю, с нулевым показателем равна единице. |
Примеры:
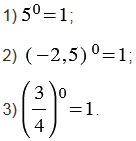
Возведение степени в степень
Для любого числа 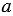 и любых натуральных чисел и любых натуральных чисел 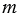 и и 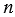 справедливо равенство: справедливо равенство: 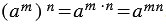 . . |
Правило возведения степени в степень:
| при возведении степени в степень показатели перемножают, а основание оставляют прежним. |
Пример:
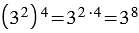 .
.
Возведение произведения в степень
|
Для любых чисел |
Аналогичное свойство справедливо и для произведения трех и более множителей: 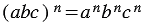 .
.
Правило возведения произведения в степень:
| при возведении произведения в степень каждый множитель возводят в эту степень и полученные результаты перемножают. |
Пример:
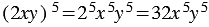 .
.
Советуем посмотреть:
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
7 класс
Номер 207, Мерзляк, Полонский, Якир, Учебник
Номер 441, Мерзляк, Полонский, Якир, Учебник
Номер 467, Мерзляк, Полонский, Якир, Учебник
Номер 536, Мерзляк, Полонский, Якир, Учебник
Номер 727, Мерзляк, Полонский, Якир, Учебник
Номер 785, Мерзляк, Полонский, Якир, Учебник
Номер 949, Мерзляк, Полонский, Якир, Учебник
Номер 1161, Мерзляк, Полонский, Якир, Учебник
Упражнение 426, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 854, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 24, Мерзляк, Полонский, Якир, Учебник
Номер 25, Мерзляк, Полонский, Якир, Учебник
Номер 53, Мерзляк, Полонский, Якир, Учебник
Номер 69, Мерзляк, Полонский, Якир, Учебник
Номер 539, Мерзляк, Полонский, Якир, Учебник
Номер 845, Мерзляк, Полонский, Якир, Учебник
Номер 863, Мерзляк, Полонский, Якир, Учебник
Упражнение 441, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 639, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 876, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс
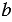 и любого натурального числа
и любого натурального числа 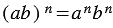 .
.