Элементы математической логики
Математическая логика - наука, которая изучает математические доказательства (логически безупречные рассуждения). Она учит, как надо рассуждать, чтобы получить верные выводы. Высказывание - это любое утверждение, относительно которого имеет смысл говорить, что оно истинно или ложно. Высказывания обозначают прописными буквами латинского алфавита: A, B, C и т.д.
Например, пишут:
А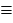 {Томбов - город России};
{Томбов - город России};
В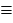 {12<11};
{12<11};
C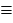 {число 4 - четное}.
{число 4 - четное}.
Любое высказывание является истинным, или ложным. Если высказывание А истинно, то будем говорить, что ему поставлено в соответствие число 1, если высказывание А ложно - то число 0. Слова "и", "или", "если..., то", тогда и только тогда" и т.п. помогают из имеющихся высказываний составлять более сложные высказывания. Примерами таких высказываний могут служить теоремы, с которыми можно ознакомится в курсе геометрии.
Рассмотрим следующее высказывание:
С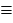 {12
{12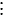 2 и 12
2 и 12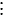 3}.
3}.
Оно составлено из двух высказываний А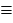 {12
{12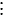 2} и В
2} и В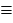 {12
{12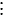 3} с помощью союза "и". Высказывание С называют конъюнкцией высказываний А и В.
3} с помощью союза "и". Высказывание С называют конъюнкцией высказываний А и В.
Определение
| Конъюнкцией (или логическим произведением) двух высказываний А и В называют высказывание, которое истинно, если каждое из высказываний А и В истинно, и ложно, если хотя бы одно из них ложно. |
Конъюнкцию высказываний А и В обозначают так: А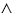 В (читают "А и В" или "А конъюнкция В"). То есть в примере выше можно сказать, что высказывание С является высказыванием А
В (читают "А и В" или "А конъюнкция В"). То есть в примере выше можно сказать, что высказывание С является высказыванием А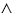 В. Также говорят, что высказывание С получено из высказываний А и В в результате логической операции конъюнкции.
В. Также говорят, что высказывание С получено из высказываний А и В в результате логической операции конъюнкции.
Логично, что истинность или ложность высказывания А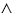 В зависит от истинности или ложности высказываний А и В. Эту зависимость удобно представить в виде таблицы, которую называют таблицей истинности:
В зависит от истинности или ложности высказываний А и В. Эту зависимость удобно представить в виде таблицы, которую называют таблицей истинности:
| А | В | А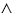 В В |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Определение
| Дизъюнкцией (или логической суммой) двух высказываний А и В называют высказывание, которое истинно, если хотя бы одно из высказываний А или В истинно, и ложно, если они оба ложны. |
Дизъюнкцию высказываний А и В обозначают так: А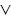 В (читают "А или В" или "А дизъюнкция В"). Таблица истинности для дизъюнкции:
В (читают "А или В" или "А дизъюнкция В"). Таблица истинности для дизъюнкции:
| А | В | А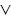 В В |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Определение
Импликацией (или логическим следованием) двух высказываний А и В называют такое высказывание А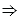 В (читают: "если А, то В"), которое ложно при условии, что высказывание А истинно, а высказывание В ложно, а во всех остальных случаях оно истинно. В (читают: "если А, то В"), которое ложно при условии, что высказывание А истинно, а высказывание В ложно, а во всех остальных случаях оно истинно. |
В импликации А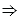 В высказывание А называют условием, а высказывание В - выводом. Таблица истинности для импликации:
В высказывание А называют условием, а высказывание В - выводом. Таблица истинности для импликации:
| А | В | А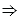 В В |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Определение
| Высказывания А и В называют логически эквивалентными, если они или оба истинны, или оба ложны |
Пишут А = В. Иными словами: А = В тогда и только тогда, если А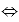 В является истинным высказыванием.
В является истинным высказыванием.
Советуем посмотреть:
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Правило встречается в следующих упражнениях:
8 класс
Номер 1, Мерзляк, Полонский, Якир, Учебник
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник