Координатная плоскость

Указать положение точки на плоскости можно с помощью координат. Для этого проведем на плоскости две перпендикулярные координатные прямые так, чтобы их начала отсчета совпадали.

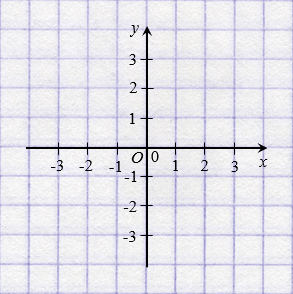
Эти прямые называют осями координат, точку их пересечения О - начало отсчета.

Горизонтальная ось - ось абсцисс, обозначают буквой , поэтому еще называют ось  , пишут: .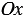

Вертикальная ось - ось ординат, обозначают буквой , поэтому еще называют ось , пишут: .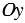

Оси и вместе образуют прямоугольную систему координат на плоскости. Плоскость, на которой выбрана система координат, называют координатной плоскостью.

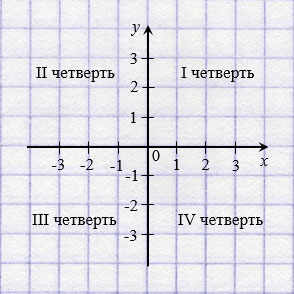
Координатные оси разбивают плоскость на четыре части, которые называют координатными четвертями и нумеруют так, как показано на рисунке ниже.

Отметим на координатной плоскости точку А. Проведем через нее прямую АВ, перпендикулярную оси абсцисс (АВ 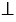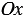), и прямую АС, перпендикулярную оси ординат (АС ).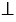

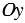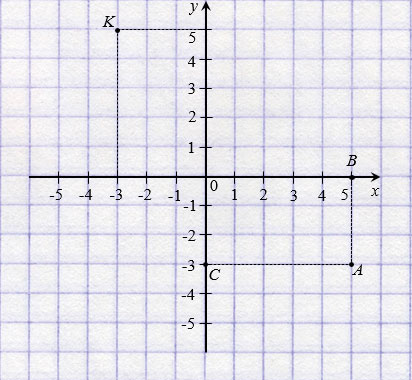
Точка В на оси имеет координату 5, а точка С на оси - координату 3 . Число 5 называют абсциссой точки А, число  3 - ординатой точки А. Числа 5 и 3 однозначно определяют положение точки А на координатной плоскости, поэтому их называют координатами точки А и записывают: А(5; 3).

Обратите внимание, записывая координаты точки, абсциссу всегда ставят на первое место, а ординату - на второе. Если числа 5 и 3 поменять местами, то получим координаты другой точки - точки К(3; 5) (смотри рисунок выше).

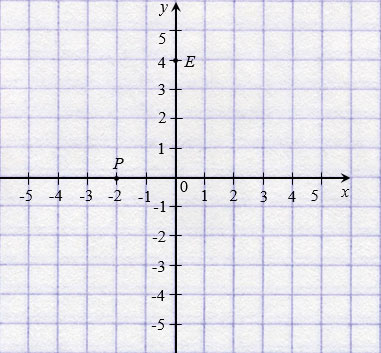
У начала координат абсцисса и ордината равны нулю, записывают так: О(0; 0). Если точка лежит на оси абсцисс, то ее ордината равна нулю, а если на оси ординат, то нулю равна ее абсцисса. На рисунке ниже: Р(2; 0); Е(0; 4).

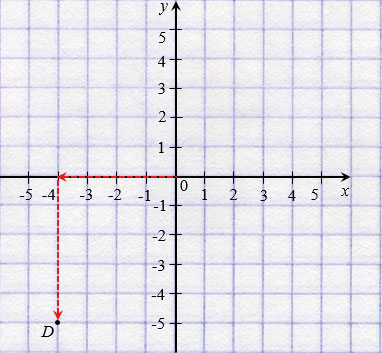
Чтобы попасть в точку D с координатами (4; 5), нужно сначала пройти по оси от начала отсчета влево на 4 единицы, а потом - на 5 единиц вниз.

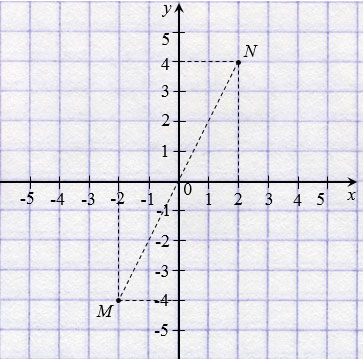
Две точки с противоположными абсциссами и ординатами симметричны относительно начала координат.

На рисунке ниже точки N(2; 4) и М(2; 4) симметричны относительно начала координат.

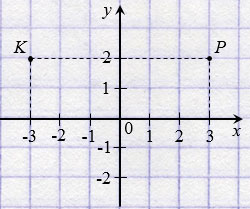
Две точки, имеющие равные ординаты и противоположные абсциссы, симметричны относительно оси ординат.

На рисунке ниже точки Р(3; 2) и К(3; 2) симметричны относительно оси ординат.

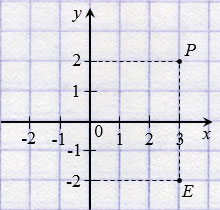
Две точки, имеющие равные абсциссы и противоположные ординаты, симметричны относительно оси абсцисс.

На рисунке ниже точки Р(3; 2) и Е(3; 2) симметричны относительно оси абсцисс.