Связи между величинами. Функция, ее свойства

В окружающем нас мире мы часто встречаемся с зависимостями между различными величинами. Например, периметр квадрата зависит от длины его стороны, площадь круга зависит от длины его радиуса, объем прямоугольного параллелепипеда зависит от трех его измерений (длины, ширины и высоты).

Рассмотрим несколько примеров.

Пример 1. Периметр квадрата изменяется, если изменяется его сторона. Если 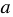- сторона квадрата, а периметр - 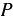, то зависимость значения переменной 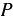от значения переменной 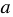(коротко говорят: зависимость переменной 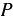от переменной 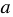) задается формулой: .

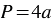С помощью этой формулы можно, выбрав произвольную длину стороны квадрата, найти соответствующее значение периметра квадрата. Поэтому переменную 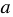называют независимой переменной, а переменную 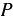- зависимой переменной.

Обратите внимание, эта формула задает правило, с помощью которого по значению независимой переменной можно однозначно найти значение зависимой переменной.

Пример 2. На рисунке ниже изображен график зависимости температуры воздуха 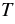от времени суток .

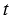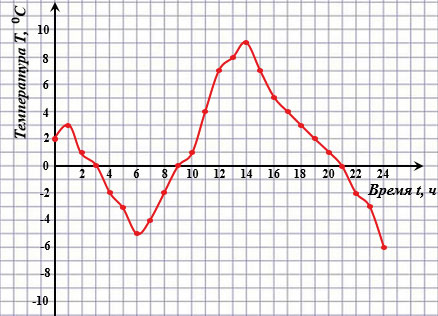
С помощью этого графика для каждого момента времени 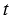(в часах) можно найти соответствующую температуру 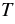(в градусах Цельсия). Значит, величина 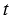является независимой переменной, а величина 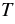- зависимой.

Обратите внимание, этот график задает правило, с помощью которого по значению независимой переменной можно однозначно найти значение зависимой переменной.

Мы рассмотрели две различные модели зависимостей, при этом для каждой из них выполняется следующее:

Как правило, независимую переменную обозначают буквой 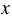, зависимую - буквой 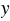, функцию - буквой 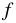. Если переменная 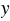зависит от переменной 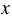, то этот факт обозначают так: 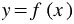(читают: "игрек равен эф от икс").

Независимую переменную еще называют аргументом функции.

Все значения, которые принимает независимая переменная (аргумент), образуют область определения функции. Область определения функции принято обозначать символом \(D(f)\). Так, в примере 1 областью определения функции являются все положительные числа; в примере 2 - все неотрицательные числа, не превосходящие 24.

Для функции 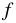каждому значению аргумента 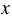соответствует некоторое значение зависимой переменной 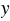. Значение зависимой переменной также называют значением функции. Запись 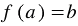обозначает то, что значению 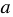аргумента соответствует значение 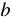функции.

Все значения, которые принимает зависимая переменная, образуют область значений функции. Область значений функции принято обозначать символом \(E(f)\). Так, в примере 1 область значений функции - это все положительные числа, в примере 2 - все числа не меньшие 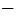6 и не большие 9.

Свойства функции

1. Нули функции - значения аргумента, при которых функция обращается в нуль.

2. Промежутки знакопостоянства - промежутки, на которых функция сохраняет знак (на промежутках, расположенных выше оси \(x\) функция принимает положительные значения, на промежутках, расположенных ниже оси \(x\) функция принимает отрицательные значения).

3. Промежутки монотонности функции - промежутки возрастания и убывания функции.

Функция называется возрастающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.

Функция называется убывающей на некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

По-другому можно сказать, что функция \(y = f(x)\) называется возрастающей  на некотором промежутке, если для любых \(x_1\) и \(x_2\)  из этого промежутка из условия \(x_2 > x_1\) следует, что \( f(x_2) > f(x_1).

Функция \(y = f(x)\) называется убывающей  на некотором промежутке, если для любых \(x_1\) и \(x_2\)  из этого промежутка из условия \(x_2 > x_1\) следует, что \( f(x_2) < f(x_1).

Если функция возрастает на всей области определения, то ее называют возрастающей функцией, а если убывает, то - убывающей функцией.

4. Четность и нечетность функции.

Функция называется четной, если выполняются следующие условия:

- область определения функции симметрична относительно оси ординат (оси \(y\);

- противоположным значениям аргумента соответствуют равные значения функции.

Пример четной функции:

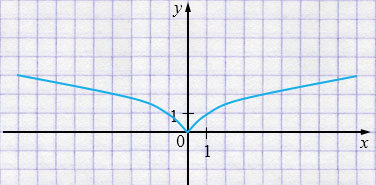
Функция называется нечетной, если выполняются следующие условия:

- область определения функции симметрична относительно начала координат;

- противоположным значениям аргумента соответствуют противоположные значения функции.

Пример нечетной функции: