График функции
Рассмотрим функцию, которая задана формулой 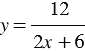 , где
, где 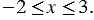 Составим таблицу для целых значений аргумента:
Составим таблицу для целых значений аргумента:
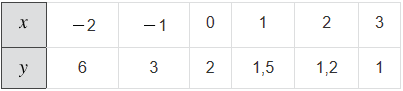
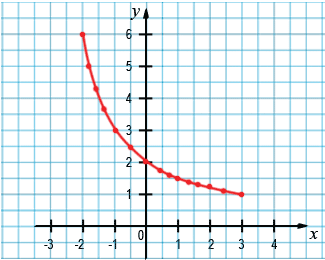
Если рассмотреть пары чисел, которые записаны в каждом столбце этой таблицы, как координаты 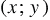 точек, то их можно отметить на координатной плоскости. При этом значения аргумента будут являться абсциссами точек, а соответствующие значения функции их ординатами.
точек, то их можно отметить на координатной плоскости. При этом значения аргумента будут являться абсциссами точек, а соответствующие значения функции их ординатами.
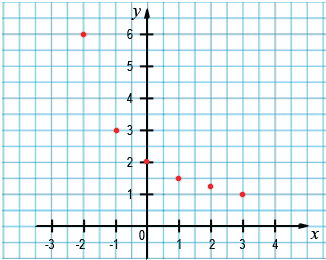
Если мы найдем значение функции при других значениях аргумента (отличных от целых значений), принадлежащих области определения функции, сможем отметить еще больше точек на координатной плоскости.
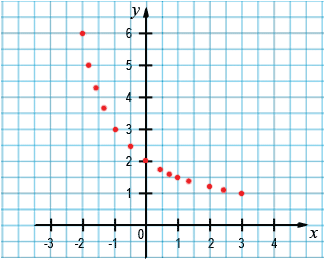
Все такие точки образуют график функции, которая задана формулой 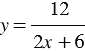 , где
, где 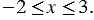 Чем больше отметим точек, которые принадлежат графику, тем точнее будет построен график функции.
Чем больше отметим точек, которые принадлежат графику, тем точнее будет построен график функции.
Графиком функции 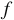 называют геометрическую фигуру, состоящую из всех тех, и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции называют геометрическую фигуру, состоящую из всех тех, и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции 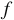 |
При этом графиком функции не всегда является линия. Но если какая-то фигура является графиком функции 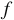 , то обязательно выполняются два условия:
, то обязательно выполняются два условия:
1) если 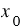 - некоторое значение аргумента, а
- некоторое значение аргумента, а 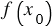 - соответствующее значение функции, то точка с координатами
- соответствующее значение функции, то точка с координатами 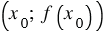 обязательно принадлежит графику;
обязательно принадлежит графику;
2) если 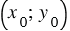 - координаты произвольно выбранной точки графика, то
- координаты произвольно выбранной точки графика, то 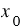 и
и 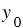 - соответствующее значения независимой и зависимой переменных функции
- соответствующее значения независимой и зависимой переменных функции 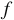 , то есть
, то есть 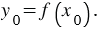
Заметим, что фигура может являться графиком некоторой функции, если любая прямая, перпендикулярная оси абсцисс, имеет с этой фигурой не более одной общей точки.
Преобразования графиков функции:
- График функции \(y=-f(x)\) можно получить из графика функции \(y=f(x)\) с помощью симметрии относительно оси \(x\).
- График функции \(y=af(x)\) можно получить из графика функции \(y=f(x)\) с помощью растяжения от оси \(x\) в \(a\) раз, если \(a>1,\) и с помощью сжатия к оси \(x\) в \(\frac{1}{a}\) раза, если \(0\lt a\lt 1\).
- График функции \(y=f(x)+n\) можно получить из графика функции \(y=f(x)\) с помощью параллельного переноса вдоль оси \(y\) на \(n\) единиц вверх, если \(n>0,\) или на \(-n\) единиц вниз, если \(n<0.\)
- График функции \(y=f(x-m)\) можно получить из графика функции \(y=f(x)\) с помощью параллельного переноса вдоль оси \(x\) на \(m\) единиц вправо, если \(m>0\), или на \(-m\) единиц влево, если \(m<0\).
- График функции \(y=f(x-m)+n\) можно получить из графика функции функции \(y=f(x)\) с помощью двух параллельных переносов: сдвига вдоль оси \(x\) на \(m\) единиц вправо, если \(m>0\), или на \(-m\) единиц влево, если \(m<0\), и сдвига вдоль оси \(y\) на на \(n\) единиц вверх, если \(n>0,\) или на \(-n\) единиц вниз, если \(n<0.\)
Советуем посмотреть:
Связи между величинами. Функция, ее свойства
Линейная функция, ее график и свойства
Функции y=x^-1 и y= x^-2 и их свойства
Квадратичная функция и её график
Дробно-линейная функция и ее график
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
7 класс
Номер 824, Мерзляк, Полонский, Якир, Учебник
Номер 830, Мерзляк, Полонский, Якир, Учебник
Номер 1211, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Номер 4, Мерзляк, Полонский, Якир, Учебник
Упражнение 292, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 379, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 441, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 511, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 579, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 63, Мерзляк, Полонский, Якир, Учебник
Номер 308, Мерзляк, Полонский, Якир, Учебник
Номер 332, Мерзляк, Полонский, Якир, Учебник
Номер 337, Мерзляк, Полонский, Якир, Учебник
Номер 10, Мерзляк, Полонский, Якир, Учебник
Номер 11, Мерзляк, Полонский, Якир, Учебник
Номер 363, Мерзляк, Полонский, Якир, Учебник
Номер 882, Мерзляк, Полонский, Якир, Учебник
Упражнение 1097, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1169, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс