Введение в алгебру

В курсе математики были изучены буквенные выражения, в частном случае формулы и уравнения. Например, буквенными выражениями являются записи:

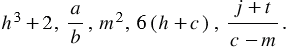
Выражение, которое состоит из одной буквы, является буквенным выражением, при этом запись, которая состоит из чисел, букв, скобок и знаков арифметических действий, может не являться буквенным выражением. Примером записи, которая является бессмысленным набором символов, может быть запись  .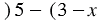

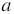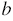Мы помним, что если длинны смежных сторон прямоугольника равны и , то его площадь выражается буквенным выражением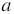 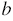. Пусть длина прямоугольника равна 4 единицам длины, а ширина - 5 единицам длины, тогда если вместо букв мы подставим данные числа, то получим числовое выражение 4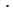5. В данном случае площадь прямоугольника будет равна 20 квадратных единиц длины. Число 20 называют значением числового выражения 4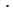5. При этом очевидно, что буквы 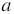и 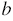можно подставлять и другие числа (в зависимости данных параметров прямоугольника), поэтому эти буквы называют переменными, а само буквенное выражение - выражением с переменными (или с переменной, если она одна).

Рассмотрим выражение 5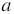 + 1. Если переменную 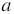заменить, например, числом 4, то получим числовое выражение 5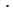4 + 1. При этом говорят, что 4 - значение переменной 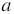, а число 21 - значение выражения 5 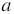+ 1 при 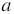= 4.

Числовые выражения и выражения с переменными называют алгебраическими выражениями. Алгебраические выражения, которые не содержат деления на выражения с переменными, называют целыми выражениями.

Например, выражения 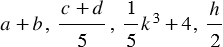являются целыми выражениями. А выражения  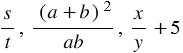не являются целыми.