Разложение многочленов на множители
Разложение многочлена на множители - это представление многочлена в виде произведения нескольких многочленов.
Вынесение общего множителя за скобки
Мы помним, что для любых рациональных чисел 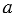 ,
, 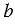 и
и 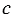 выполняется равенство
выполняется равенство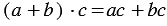 (распределительное свойство умножения относительно сложения). Данную идею можно использовать при разложении многочлена на множители.
(распределительное свойство умножения относительно сложения). Данную идею можно использовать при разложении многочлена на множители.
Например, разложим на множители многочлен
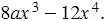
Очевидно, что каждый его член можно заменить произведением двух множителей, один из которых равен 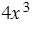 :
:
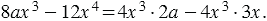
На основе свойства, записанного выше, мы можем представить данный многочлен в виде произведения двух множителей:
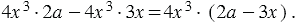
Значит, мы можем записать:
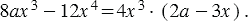
Мы разложили многочлен на множители с помощью вынесения общего множителя.
Пример: Разложим на множители многочлен
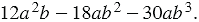
Мы видим, что члены данного многочлена имеют разные общие множители 6, 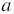 ,
, 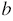 ,
, 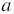
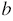 , 6
, 6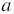
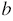 . Каждый из этих общих множителей мы можем вынести за скобки, но обычно общий множитель выбирают таким образом, чтобы члены многочлена, которые останутся в скобках, не содержали общего буквенного множителя, а модули их коэффициентов не имели общих натуральных делителей, кроме 1.
. Каждый из этих общих множителей мы можем вынести за скобки, но обычно общий множитель выбирают таким образом, чтобы члены многочлена, которые останутся в скобках, не содержали общего буквенного множителя, а модули их коэффициентов не имели общих натуральных делителей, кроме 1.
В нашем многочлене модули коэффициентов равны 12, 18 и 30, а их наибольший общий делитель 6, поэтому коэффициент общего множителя будет равен или 6 или 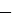 6. Все члены многочлена содержат переменные
6. Все члены многочлена содержат переменные 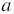 и
и 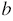 , имея первую, вторую и третью степени. Но вынести мы можем наименьшую степень переменной, в нашем случаем и переменную
, имея первую, вторую и третью степени. Но вынести мы можем наименьшую степень переменной, в нашем случаем и переменную 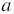 и переменную
и переменную 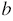 выносим в первой степени. Значит, за скобки можно вынести одночлен 6
выносим в первой степени. Значит, за скобки можно вынести одночлен 6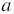
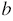 или (
или (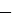 6
6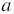
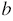 ). Например вынесем 6
). Например вынесем 6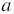
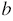 , получим:
, получим:
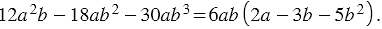
Метод группировки
Попробуем разложить на множители многочлен 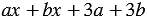 .
.
Его члены не имеют общего множителя, но их можно сгруппировать так, что слагаемые в каждой группе будут иметь общий множитель и его можно будет вынести за скобки:
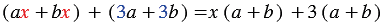 .
.
Мы получили выражение, в котором оба слагаемых имеют общий множитель 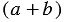 , вынесем его за скобки:
, вынесем его за скобки:
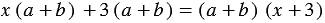 .
.
Получается, 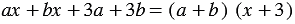 .
.
Описанный выше прием разложения многочлена на множители называют методом группировки.
Обратите внимание, совсем необязательно группировать те слагаемые, которые расположены рядом. Так, в многочлене 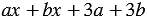 , можно сгруппировать первое слагаемое с третьим, а второе - с четвертым, и результат разложения на множители, учитывая переместительное свойство умножения, получится тот же:
, можно сгруппировать первое слагаемое с третьим, а второе - с четвертым, и результат разложения на множители, учитывая переместительное свойство умножения, получится тот же:
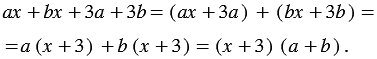
Пример: Разложите на множители трехчлен 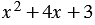 .
.
Сначала представим слагаемое 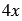 в виде суммы
в виде суммы 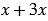 , получим многочлен:
, получим многочлен:
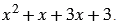
Далее группируем слагаемые полученного многочлена следующим образом:
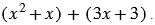
Первая группа слагаемых имеет общий множитель 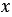 , вторая группа слагаемых имеет общий множитель 3. Вынесем каждый из этих множителей, в соответствующей им группе слагаемых, за скобки:
, вторая группа слагаемых имеет общий множитель 3. Вынесем каждый из этих множителей, в соответствующей им группе слагаемых, за скобки:
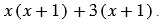
Мы получили выражение, в котором оба слагаемых имеют множитель  , вынесем его за скобки:
, вынесем его за скобки:
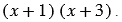
Получается, трехчлен 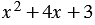 мы представили в виде произведения двух множителей:
мы представили в виде произведения двух множителей: 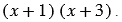
Итак, при разложении многочлена на множители можно использовать следующие способы:
- вынесение общего множителя за скобки;
- метод группировки;
- применение формул сокращенного умножения.
Однако есть много многочленов, для разложения которых на множители надо применить несколько способов. Как правило при разложении многочлена на множители нужно соблюдать следующий алгоритм:
1) если это возможно, то разложение надо начинать с вынесения общего множителя за скобки;
2) проверить, можно ли применить формулы сокращенного умножения;
3) если не удается применить формулы, то пробуем воспользоваться методом группировки.
Советуем посмотреть:
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
7 класс
Номер 451, Мерзляк, Полонский, Якир, Учебник
Номер 464, Мерзляк, Полонский, Якир, Учебник
Номер 532, Мерзляк, Полонский, Якир, Учебник
Номер 623, Мерзляк, Полонский, Якир, Учебник
Номер 712, Мерзляк, Полонский, Якир, Учебник
Номер 5, Мерзляк, Полонский, Якир, Учебник
Номер 6, Мерзляк, Полонский, Якир, Учебник
Упражнение 670, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 733, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1003, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 96, Мерзляк, Полонский, Якир, Учебник
Номер 118, Мерзляк, Полонский, Якир, Учебник
Номер 123, Мерзляк, Полонский, Якир, Учебник
Номер 766, Мерзляк, Полонский, Якир, Учебник
Упражнение 23, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 48, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 64, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 158, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 800, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение стр. 255, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс