Положительные и отрицательные числа. Координаты на прямой
Рассмотрим горизонтальную прямую МN и отметим на этой прямой точку О. Точку О называют началом отсчета, ей соответствует число 0 и она разбивает прямую MN на два дополнительных луча: ОМ и ОN. Отметим на луче ОN точку А, которой соответствует число +1, т.е. зададим единичный отрезок. Тогда положение точки на каждом из лучей задается ее координатой. Чтобы отличать друг от друга координаты на этих лучах, условились ставить перед координатами на одном луче знак "+", т.е. луч ОN задает положительное направление, а перед координатами на другом луче знак " - ", т.е. луч ОМ задает отрицательное направление. Положительное направление указывают стрелкой.

Числа, которые пишут со знаком "+", например, +2; +4,5; +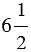 , но обычно для краткости в записи этот знак не пишут, т.е. вместо +2; +4,5; +
, но обычно для краткости в записи этот знак не пишут, т.е. вместо +2; +4,5; +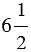 , пишут просто 2; 4,5;
, пишут просто 2; 4,5; 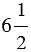 , называют положительными. Числа, которые пишут со знаком " - ", например, -3; -7,2; -
, называют положительными. Числа, которые пишут со знаком " - ", например, -3; -7,2; -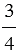 , называют отрицательными (если число отрицательное, то знак " - " писать обязательно).
, называют отрицательными (если число отрицательное, то знак " - " писать обязательно).
Определение:
| Координатная прямая - это прямая, на которой задано начало отсчета, единичный отрезок и направление. |
На рисунке выше прямая МN - координатная прямая, т.к. на ней задано начало отсчета - точка О, единичный отрезок ОА и направление - вправо.
Число 0 не является ни положительным числом, ни отрицательным числом. Оно отделяет положительные и отрицательные числа друг от друга. Все положительные числа и ноль называют неотрицательными числами, а все отрицательные числа и ноль, называют неположительными числами.
Прямые могут находится в различных положениях, поэтому дополнительные лучи могут идти не только влево и вправо, но и в других направлениях. Самые распространенные направления дополнительных лучей: влево и вправо, когда прямая расположена горизонтально (рисунок выше), вверх и вниз, когда прямая расположена вертикально (рисунок ниже).
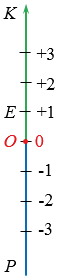
Определение:
| Координата точки - число, показывающее положение точки на прямой. |

На рисунке выше изображена горизонтальная координатная прямая с началом отсчета О и единичным отрезком ОА. Точка В изображает число -1, значит, точка В имеет координату -1, записывают так: В(-1). Аналогично можно записать: А(1), D(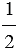 ), М(
), М(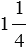 ), Р(2), С(-1,5), К(-2).
), Р(2), С(-1,5), К(-2).
Точки Р и К изображают числа 2 и - 2 соответственно. Эти точки лежат по разные стороны от начала отсчета, но на одинаковом расстоянии от него. Числа 2 и -2 называют противоположными.
Определение:
| Противоположные числа - это два числа, которые отличаются друг от друга только знаками. |
Например, противоположными будут: 8 и -8; 3,4 и -3,4; 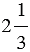 и -
и -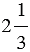 . Для каждого числа есть только одно число противоположное ему. Число 0 противоположно самому себе.
. Для каждого числа есть только одно число противоположное ему. Число 0 противоположно самому себе.
Выражение 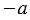 означает, что записано число, противоположное числу
означает, что записано число, противоположное числу 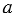 . Приписав перед число знак " - ", например к положительному числу 10, получим противоположное ему число -10. Так же с помощью знака " - " из отрицательного числа -10 можно получить противоположное ему число 10, т.е. -(-10) = 10. В общем виде можем записать:
. Приписав перед число знак " - ", например к положительному числу 10, получим противоположное ему число -10. Так же с помощью знака " - " из отрицательного числа -10 можно получить противоположное ему число 10, т.е. -(-10) = 10. В общем виде можем записать: 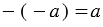 . Обратите внимание, скобки при записи
. Обратите внимание, скобки при записи 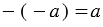 обязательны, запись
обязательны, запись 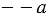 не имеет смысла.
не имеет смысла.
Определение:
| Целые числа - это все натуральные числа, противоположные им числа и ноль. |
Числа -25, 0, 14 - целые числа, числа 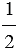 ; -2,5;
; -2,5; 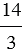 - не являются целыми, их называют дробными числами. Вместе целые и дробные числа образуют рациональные числа.
- не являются целыми, их называют дробными числами. Вместе целые и дробные числа образуют рациональные числа.
Обратите внимание, разные координатные прямые могут иметь разные единичные отрезки, так, на рисунке ниже, координатная прямая АВ имеет единичный отрезок, равный 1 клетке, прямая РК имеет единичный отрезок, равный 2 клетки, а прямая МN имеет единичный отрезок, равный 3 клетки.

Изменение величин
| Увеличение любой величины можно выразить положительными числами, а уменьшение - отрицательными. |
Примером изменения величины может служит изменение температуры в течение дня. Рассмотрим как изменялись показания термометров в течение дня:
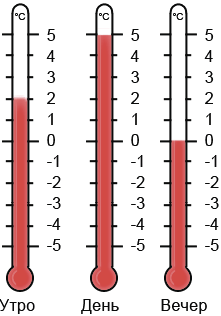
Утром температура воздуха была 2°С, днем - 5°С, вечером - 0°С. То есть за первую половину дня температура повысилась на 3°С, а к вечеру понизилась на 5°С. Учитывая вышесказанное, мы можем выразить первое изменение - повышение температуры - положительным числом 3°С, при этом говорим, что изменение температуры равно 3°С или +3°С. Второе изменение - понижение температуры - отрицательным числом -5°С, при этом говорим, что изменение температуры равно -5°С.
Советуем посмотреть:
Свойства действий с рациональными числами
Правило встречается в следующих упражнениях:
5 класс
Задание 4, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Номер 956, Мерзляк, Полонский, Якир, Учебник
Номер 1010, Мерзляк, Полонский, Якир, Учебник
Номер 1078, Мерзляк, Полонский, Якир, Учебник
Задание 1315, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1318, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 579, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 4.6, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 4.16, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 4.283, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание П.31, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 59, Мерзляк, Полонский, Якир, Учебник
Номер 585, Мерзляк, Полонский, Якир, Учебник
Номер 595, Мерзляк, Полонский, Якир, Учебник
Номер 684, Мерзляк, Полонский, Якир, Учебник
Номер 1024, Мерзляк, Полонский, Якир, Учебник
Номер 1091, Мерзляк, Полонский, Якир, Учебник
Номер 1092, Мерзляк, Полонский, Якир, Учебник
Номер 1125, Мерзляк, Полонский, Якир, Учебник
Упражнение 647, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1155, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 8, Мерзляк, Полонский, Якир, Учебник
Номер 207, Мерзляк, Полонский, Якир, Учебник
Номер 209, Мерзляк, Полонский, Якир, Учебник
Номер 9, Мерзляк, Полонский, Якир, Учебник
Упражнение 300, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 537, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 544, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 748, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 763, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 792, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс