Способы задания функции

Функция считается заданной, если указаны её область определения и правила, с помощью которого можно по каждому значению независимой переменной найти значение зависимой переменной.

Описательный способ - способ, при котором правило задается с помощью слов.

Пример 1.Пусть независимая переменная принимает любые значения, отличные от 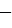1. Значения зависимой переменной находим по такому правилу: каждое значение зависимой переменной соответствует числу обратному сумме 1 и независимой переменной. То есть мы задали некоторую функцию 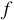, область определения которой являются все числа кроме 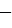1. Например,

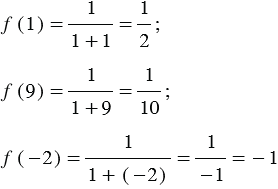
и т.п.

Аналитический способ - способ, при котором правило задается с помощью формулы.

Пример 2. Если в первом примере независимую переменную обозначит буквой 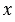, а зависимую - буквой 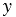, указать область определения 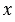- любое число, отличное от 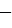1, тогда формула 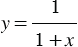задает вышеописанную функцию.

Заметим, что в случае, если функция задана формулой, в которой правая часть является целым выражением, и при этом не указана область определения, условились считать, что областью определения такой функции являются все числа.

Табличный способ - способ, при котором правило задается с помощью таблицы. При этом в первой строке указывается значения независимой переменной и составляют область определения функции, а во второй - зависимой переменной.

Пример 3.

Данная таблица задает функцию и позволяет по указанному значению аргумента найти соответствующее значение функции. Данный способ удобно использовать, когда область определения функции состоит из нескольких чисел.

Графический способ - способ, при котором правило задается с помощью графика (см. данную статью).