Симметрии фигур (осевая, центральная, поворотная, переносная)
Осевая симметрия
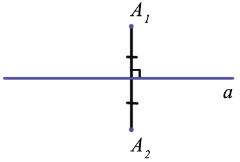
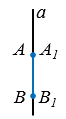
Если прямая 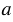 проходит через середину отрезка А1А2 и перпендикулярна к нему, то точки А1 и А2 называются симметричными относительно прямой
проходит через середину отрезка А1А2 и перпендикулярна к нему, то точки А1 и А2 называются симметричными относительно прямой 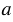 . Каждая точка прямой
. Каждая точка прямой 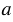 симметрична самой себе.
симметрична самой себе.
Фигура называется симметричной относительно прямой 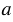 , если для каждой точки фигуры симметричная ей точка относительно прямой
, если для каждой точки фигуры симметричная ей точка относительно прямой 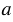 также принадлежит этой фигуре. Прямая
также принадлежит этой фигуре. Прямая 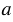 - ось симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.
- ось симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.
Пример (синим цветом обозначены оси симметрии):
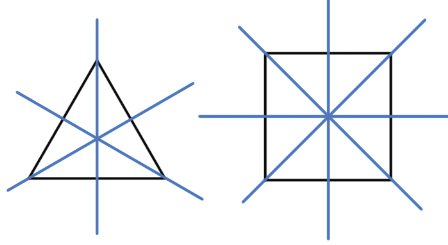
Имеются фигуры, у которых нет ни одной оси симметрии.
Ось симметрии точек А и А1 является серединным перпендикуляром к отрезку АА1. Также помним, что каждая точка серединного перпендикуляра к отрезку равноудалена от его концов, поэтому каждая точка оси симметрии двух точек равноудалена от этих точек.
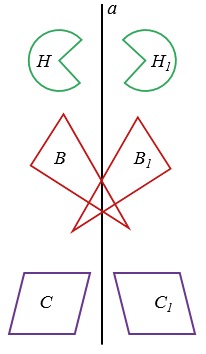
Две фигуры называются симметричными относительно прямой, если каждая точка одной фигуры симметрична некоторой точке другой фигуры, и обратно. Данная прямая называется осью симметрии этих фигур. На рисунке ниже фигуры H и Н1, В и В1, С и С1 симметричны относительно прямой 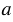 .
.
Свойства осевой симметрии
Если 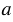 - некоторая прямая, то каждой точке А плоскости симметрична относительно прямой
- некоторая прямая, то каждой точке А плоскости симметрична относительно прямой 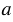 только одна точка А1. Говорят, что прямая
только одна точка А1. Говорят, что прямая 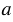 задает на плоскости осевую симметрию с осью
задает на плоскости осевую симметрию с осью 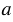 .
.
В то случае, когда осевая симметрия задана, то для каждой фигуры существует симметричная ей фигура относительно оси 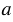 .
.
|
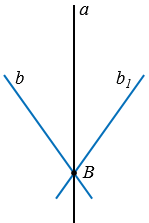
10. Если две прямые
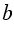 и и 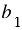 симметричны относительно оси а, то они либо параллельны, либо их точка пересечения лежит на оси симметрии симметричны относительно оси а, то они либо параллельны, либо их точка пересечения лежит на оси симметрии 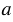 . . |
Действительно, если прямая 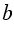 пересекает ось а в точке В, то точка В симметрична самой себе и симметрична какой-либо точке на прямой
пересекает ось а в точке В, то точка В симметрична самой себе и симметрична какой-либо точке на прямой 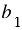 . Тогда прямая
. Тогда прямая 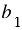 также пересекает ось а в точке В (смотри рисунок ниже).
также пересекает ось а в точке В (смотри рисунок ниже).
|
20. Расстояние между точками А и В равно расстоянию между симметричными им точками А1 и В1.
|
Доказательство:
1 случай
Пусть А и В — две точки, а А1 и В1 — симметричные им точки относительно прямой 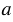 .
.
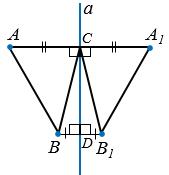
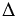 ВСD =
ВСD = 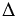 В1СD по двум катетам: СВ - общий катет, ВD = В1D, значит, ВС = В1С). Тогда CD — высота и биссектриса, проведённая к его основанию ВВ1. Следовательно, в
В1СD по двум катетам: СВ - общий катет, ВD = В1D, значит, ВС = В1С). Тогда CD — высота и биссектриса, проведённая к его основанию ВВ1. Следовательно, в 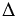 AСB и
AСB и 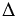 A1СB1
A1СB1 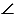 AСB =
AСB = 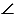 A1СB1 (т.к. СD - биссектриса
A1СB1 (т.к. СD - биссектриса 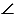 ВСВ1, тогда
ВСВ1, тогда 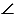 ВСD =
ВСD = 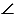 В1СD, а
В1СD, а 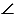 AСB и
AСB и 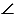 A1СB1 смежные с углами
A1СB1 смежные с углами 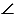 ВСD и
ВСD и 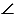 В1СD).
В1СD). 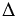 ACB =
ACB = 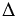 A1CB1 по первому признаку, поэтому их соответственные стороны АВ и А1В1 равны. Получается, расстояние между точками А и В равно расстоянию между симметричными им точками А1 и В1, что и требовалось доказать.
A1CB1 по первому признаку, поэтому их соответственные стороны АВ и А1В1 равны. Получается, расстояние между точками А и В равно расстоянию между симметричными им точками А1 и В1, что и требовалось доказать.2 случай
Пусть А и В — две точки, а А1 и В1 — симметричные им точки относительно прямой 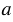 .
.
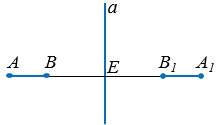
Доказательство:
АВ = АЕ - ВЕ и А1В1 = А1Е - В1Е, при этом АЕ = А1Е и ВЕ = В1Е по определению осевой симметрии, следовательно, АВ = А1В1, значит, расстояние между точками А и В равно расстоянию между симметричными им точками А1 и В1, что и требовалось доказать.
3 случай
Пусть А и В — две точки, а А1 и В1 — симметричные им точки относительно прямой 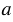 .
.
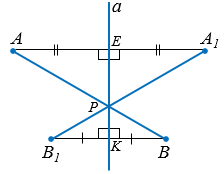
 АРЕ =
АРЕ = 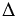 А1РЕ по двум катетам (АЕ = А1Е, ЕР - общий катет), поэтому их соответственные стороны АР и А1Р равны.
А1РЕ по двум катетам (АЕ = А1Е, ЕР - общий катет), поэтому их соответственные стороны АР и А1Р равны.
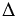 ВРK =
ВРK = 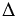 В1РK по двум катетам (АЕ = А1Е, ЕР - общий катет), поэтому их соответственные стороны BР и В1Р равны.
В1РK по двум катетам (АЕ = А1Е, ЕР - общий катет), поэтому их соответственные стороны BР и В1Р равны.
АВ = АР + ВР и А1В1 = А1Р + В1Р, значит, АВ = А1В1, следовательно, расстояние между точками А и В равно расстоянию между симметричными им точками А1 и В1, что и требовалось доказать.
4 случай
Пусть А и В — две точки, а А1 и В1 — симметричные им точки относительно прямой 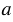 .
.
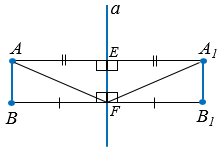
Доказательство:
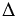 АЕF =
АЕF = 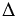 АВF по второму признаку (АF - общая,
АВF по второму признаку (АF - общая, 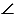 ЕАF =
ЕАF = 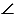 АFВ и
АFВ и 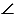 ЕFА =
ЕFА = 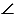 FАВ как накрест лежащие углы при пересечении параллельных прямых АА1 и ВВ1 секущей АF), значит, АВ = ЕF.
FАВ как накрест лежащие углы при пересечении параллельных прямых АА1 и ВВ1 секущей АF), значит, АВ = ЕF.
Аналогично, 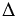 А1ЕF =
А1ЕF = 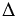 А1В1F по второму признаку (А1F - общая,
А1В1F по второму признаку (А1F - общая, 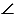 ЕА1F =
ЕА1F = 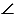 А1FВ1 и
А1FВ1 и 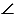 ЕFА1 =
ЕFА1 = 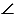 FА1В1 как накрест лежащие углы при пересечении параллельных прямых АА1 и ВВ1 секущей А1F), значит, А1В1 = ЕF.
FА1В1 как накрест лежащие углы при пересечении параллельных прямых АА1 и ВВ1 секущей А1F), значит, А1В1 = ЕF.
Итак, АВ = ЕF и А1В1 = ЕF, поэтому АВ = А1В1, следовательно, расстояние между точками А и В равно расстоянию между симметричными им точками А1 и В1, что и требовалось доказать.
4 случай
Пусть А и В — две точки, а А1 и В1 — симметричные им точки относительно прямой 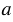 .
.
Доказательство:
Точки А и А1, В и В1 совпадают, значит, совпадают отрезки АВ и А1В1, следовательно, расстояние между точками А и В равно расстоянию между симметричными им точками А1 и В1, что и требовалось доказать.
Центральная симметрия
Точки А1 и А2 называются симметричными относительно точки О, если О - середина отрезка А1А2.
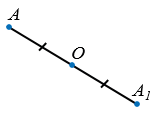
Точка О считается симметричной самой себе.
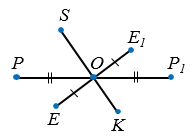
На рисунке ниже точки Е и Е1, Р и Р1 симметричны относительно точки О, а точки S и K не симметричны относительно этой точки (так как отрезки ОS и ОK не равны).
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры.
Пример (синим цветом обозначены центры симметрии):
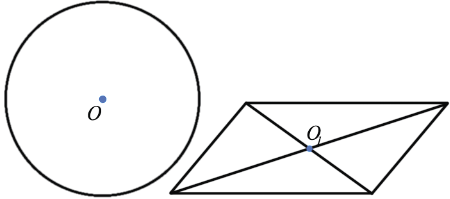
Центр симметрии окружности - ее центр, а центр симметрии параллелограмма - точка пересечения его диагоналей. Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии, у прямой их бесконечно много - любая точка прямой является ее центром симметрии. Примером фигуры не имеющей центра симметрии, является произвольный треугольник.
Поворотная симметрия
Переносная симметрия
Внутренняя симметрия
Внутренней симметрией (или симметрией) фигуры называется любое движение плоскости, отличное от тождественного преобразования, которое фигуру отображает на себя.
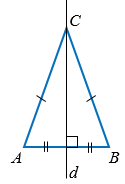
Например, равнобедренный, но не равносторонний треугольник имеет одну симметрию – это осевая симметрия относительно серединного перпендикуляра к основанию этого треугольника.
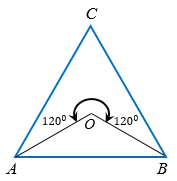
У равностороннего треугольника пять симметрий: три осевые симметрии и две поворотные симметрии вокруг центра треугольника на 120° по часовой и против часовой стрелки.
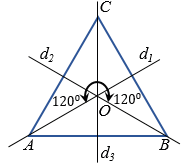
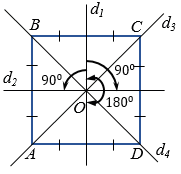
У квадрата уже семь симметрий: четыре осевые симметрии, одна центральная симметрия и две поворотные симметрии вокруг центра квадрата на 90° по часовой и против часовой стрелки.
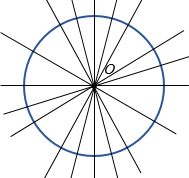
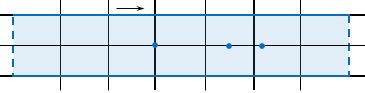
Рассмотрим две параллельные прямые и часть плоскости между ними. Такую геометрическую фигуру называют полосой. Прямые, ограничивающие полосу, называют её краями. Полоса, как и окружность, имеет бесконечно много симметрий — это и осевые, и центральные, и переносные симметрии.
Советуем посмотреть:
Правило встречается в следующих упражнениях:
7 класс
Задание 441, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 444, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 384, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 909, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 1271, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 1279, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 1282, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 1283, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 28, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник