Параллельный перенос
Если нам дан вектор  , то параллельным переносом на вектор
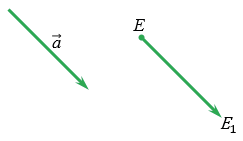
, то параллельным переносом на вектор  называется отображение плоскости на себя, при котором произвольная точка Е отображается в такую точку Е1, что
называется отображение плоскости на себя, при котором произвольная точка Е отображается в такую точку Е1, что 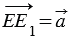 .
.
| Параллельный перенос - это частный случай движения, т.е. отображение плоскости на себя, при котором сохраняются расстояния. |
Доказательство:
Дано: точки Е и К отображаются в точки Е1 и К1 при параллельном переносе на  .
.
Доказать: параллельный перенос - движение.
Доказательство:
1 случай
Точки Е и К не лежат на одной прямой параллельной вектору  .
.
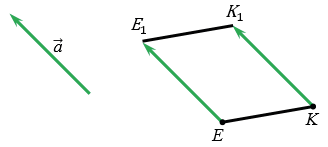
По условию точки Е и К отображаются в точки Е1 и К1 соответственно при параллельном переносе на вектор  , тогда по определению параллельного переноса
, тогда по определению параллельного переноса 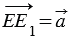 и
и 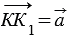 , поэтому
, поэтому  , следовательно,
, следовательно, 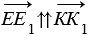 и
и 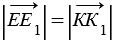 , значит, ЕЕ1
, значит, ЕЕ1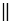 КК1 (т.к. точки Е и К не лежат на одной прямой параллельной вектору
КК1 (т.к. точки Е и К не лежат на одной прямой параллельной вектору  ) и ЕЕ1 = КК1. Следовательно, по признаку параллелограмма четырехугольник ЕЕ1К1К - параллелограмм, поэтому по свойству параллелограмма ЕК = Е1К1, т.е. расстояние между точками Е и К равно расстоянию между точками Е1 и К1. Получаем, что параллельный перенос сохраняет расстояния между точками, значит, является частным случаем движения.
) и ЕЕ1 = КК1. Следовательно, по признаку параллелограмма четырехугольник ЕЕ1К1К - параллелограмм, поэтому по свойству параллелограмма ЕК = Е1К1, т.е. расстояние между точками Е и К равно расстоянию между точками Е1 и К1. Получаем, что параллельный перенос сохраняет расстояния между точками, значит, является частным случаем движения.
2 случай
Точки Е и К лежат на одной прямой параллельной вектору  .
.
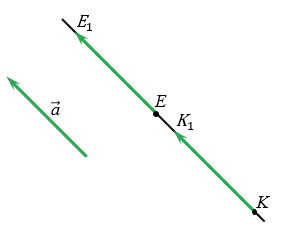
По условию точки Е и К отображаются в точки Е1 и К1 соответственно при параллельном переносе на вектор  , тогда по определению параллельного переноса
, тогда по определению параллельного переноса 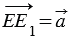 и
и 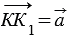 , поэтому
, поэтому  , следовательно,
, следовательно, 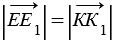 , значит, ЕЕ1 = КК1. (1)
, значит, ЕЕ1 = КК1. (1)
ЕК = КК1 + ЕК1, Е1К1 = ЕЕ1 + ЕК1, тогда, учитывая (1), получим: ЕК = Е1К1, т.е. расстояние между точками Е и К равно расстоянию между точками Е1 и К1. Получаем, что параллельный перенос сохраняет расстояния между точками, значит, является частным случаем движения.
Пример
Построить 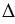 А1В1С1, который получается из
А1В1С1, который получается из 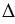 АВС параллельным переносом на вектор
АВС параллельным переносом на вектор  .
.
Дано: 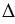 АВС, вектор
АВС, вектор  .
.
Построить: 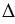 А1В1С1 параллельным переносом на вектор
А1В1С1 параллельным переносом на вектор  .
.
Решение:
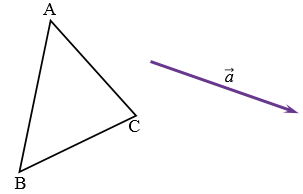
Построим точки А1, В1, С1, которые получаются из точек А, В, С соответственно, параллельным переносом на вектор  . Для этого от точек А, В и С отложим векторы, равные вектору
. Для этого от точек А, В и С отложим векторы, равные вектору  . Соединяя попарно точки А1, В1, С1 отрезками, получим искомый
. Соединяя попарно точки А1, В1, С1 отрезками, получим искомый 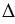 А1В1С1.
А1В1С1.
Советуем посмотреть:
Правило встречается в следующих упражнениях:
7 класс
Задание 1162, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1164, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1165, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1178, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1179, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1182, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 14, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1262, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 1279, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник