Первый признак равенства треугольников
Теорема
| Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны |
Пример:
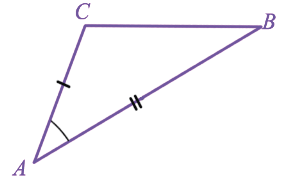
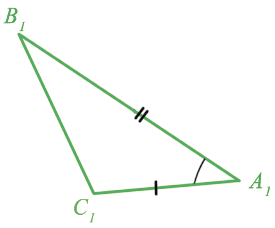
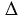 ABC =
ABC = 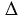 A1B1C1, так как AC = A1C1, AB =A1B1 и
A1B1C1, так как AC = A1C1, AB =A1B1 и 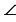 A =
A = 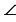 A1 (
A1 ( 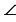 A лежит между сторонами AC и AB, а
A лежит между сторонами AC и AB, а 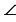 A1 между A1C1 и A1B1)
A1 между A1C1 и A1B1)
Доказательство:
Дано: 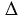 ABC,
ABC, 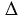 A1B1C1, AC = A1C1, AB =A1B1,
A1B1C1, AC = A1C1, AB =A1B1, 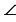 A =
A = 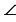 A1
A1
Доказать: 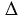 ABC =
ABC = 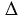 A1B1C1
A1B1C1
Доказательство:


По тому как 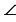 A =
A = 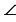 A1, можно
A1, можно 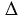 ABC наложить на
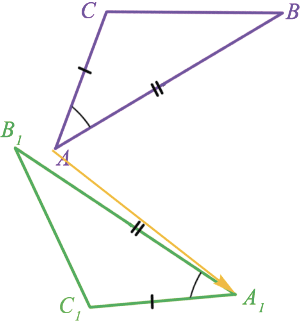
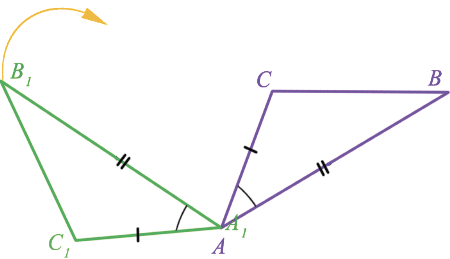
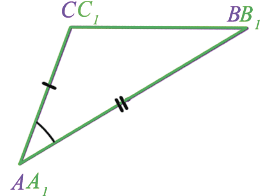
ABC наложить на 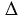 A1B1C1 так, что вершины A и A1 совместятся, а стороны AC и AB наложатся на лучи A1C1 и A1B1. Так как нам дано, что AB =A1B1, AC = A1C1, то сторона AB совместится со стороной A1B1, а сторона AC - со стороной A1C1; также совместятся точки B и B1, C и C1. Следовательно, совместятся стороны BC и B1C1. Итак,
A1B1C1 так, что вершины A и A1 совместятся, а стороны AC и AB наложатся на лучи A1C1 и A1B1. Так как нам дано, что AB =A1B1, AC = A1C1, то сторона AB совместится со стороной A1B1, а сторона AC - со стороной A1C1; также совместятся точки B и B1, C и C1. Следовательно, совместятся стороны BC и B1C1. Итак, 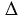 ABC и
ABC и 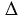 A1B1C1 полностью совместятся, значит, они равны, что и требовалось доказать.
A1B1C1 полностью совместятся, значит, они равны, что и требовалось доказать.
Советуем посмотреть:
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Построения циркулем и линейкой
Правило встречается в следующих упражнениях:
7 класс
Задание 93, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 105, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 129, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 146, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 177, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 820, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1235, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 2, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник