Свойства равнобедренного треугольника
1. Теорема
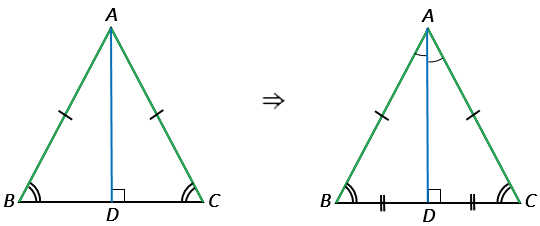
| В равнобедренном треугольнике углы при основании равны. |
Дано:  АВС - равнобедренный, ВС - основание.
АВС - равнобедренный, ВС - основание.
Доказать:  В =
В =  С.
С.
Доказательство:
Проведем биссектрису АD из вершины А к стороне ВС.
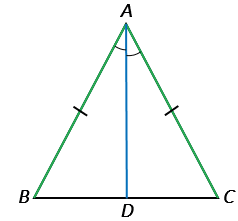
Рассмотрим  АВD и
АВD и  АСD: АВ = АС по условию (
АСD: АВ = АС по условию ( АВС - равнобедренный), АD - общая сторона,
АВС - равнобедренный), АD - общая сторона,  BAD =
BAD =  CAD, так как АD - биссектриса по построению,
CAD, так как АD - биссектриса по построению, 
 АВD =
АВD =  АСD по первому признаку равенства треугольников
АСD по первому признаку равенства треугольников 
 В =
В =  С, потому что в равных треугольниках против равных сторон лежат равные углы (
С, потому что в равных треугольниках против равных сторон лежат равные углы ( В лежит против стороны АС,
В лежит против стороны АС,  С. - против стороны АВ).
С. - против стороны АВ).
Теорема доказана.
Справедливо и обратное утверждение:
| Если в каком-либо треугольнике два угла равны, то такой треугольник равнобедренный. |
2. Теорема
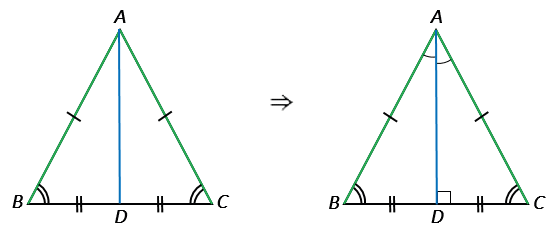
| В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой. |
Дано:  АВС - равнобедренный, ВС - основание, АD - биссектриса.
АВС - равнобедренный, ВС - основание, АD - биссектриса.
Доказать: АD - медиана и высота.
Доказательство:

Рассмотрим  АВD и
АВD и  АСD: АВ = АС по условию (
АСD: АВ = АС по условию ( АВС - равнобедренный), АD - общая сторона,
АВС - равнобедренный), АD - общая сторона,  BAD =
BAD =  CAD, так как АD - биссектриса по условию,
CAD, так как АD - биссектриса по условию, 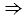
 АВD =
АВD =  АСD по первому признаку равенства треугольников
АСD по первому признаку равенства треугольников  ВD = DC и
ВD = DC и  ADВ =
ADВ =  ADС.
ADС.
Мы доказали, что ВD = DC 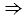 точка D - середина стороны ВС, тогда АD является медианой
точка D - середина стороны ВС, тогда АD является медианой  АВС (по определению медианы).
АВС (по определению медианы).
Мы доказали, что  ADВ =
ADВ =  ADС, причем
ADС, причем  ADВ и
ADВ и  ADС - смежные углы, поэтому
ADС - смежные углы, поэтому  ADВ +
ADВ +  ADС = 1800, тогда
ADС = 1800, тогда  ADВ =
ADВ =  ADС = 900, т.е. АD
ADС = 900, т.е. АD BC, а это означает, что AD является высотой
BC, а это означает, что AD является высотой  АВС (по определению высоты).
АВС (по определению высоты).
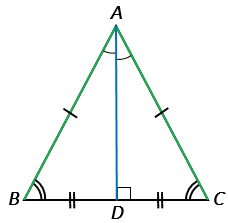
Теорема доказана.
Справедливо и обратное утверждение:
| Если в каком-либо треугольнике медиана и высота совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника. |
3. Теорема
| В равнобедренном треугольнике высота, проведённая к основанию, является медианой и биссектрисой. |
Справедливо и обратное утверждение:
| Если в каком-либо треугольнике медиана и биссектриса совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника. |
4. Теорема
| В равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой. |
Справедливо и обратное утверждение:
| Если в каком-либо треугольнике высота и биссектриса совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника. |
Важно помнить, что данные теоремы справедливы только в том случае, если высота, медиана и биссектриса равнобедренного треугольника проведены к его ОСНОВАНИЮ.
Если треугольник равносторонний, то данные теоремы справедливы для медиан, биссектрис и высот, проведенных к каждой из сторон треугольника.
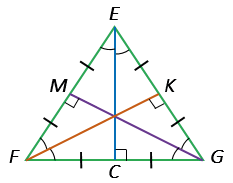
 EFG - равносторонний:
EFG - равносторонний:
- ЕС - биссектриса, медиана и высота, проведенная к стороне FG,
- FK - биссектриса, медиана и высота, проведенная к стороне ЕG,
- GM - биссектриса, медиана и высота, проведенная к стороне ЕF.
Советуем посмотреть:
Первый признак равенства треугольников
Второй признак равенства треугольников
Третий признак равенства треугольников
Построения циркулем и линейкой
Правило встречается в следующих упражнениях:
7 класс
Задание 178, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 225, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 232, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 234, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 254, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 359, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 425, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 816, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 932, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 277, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Упражнение 1146, Макарычев, Миндюк, Нешков, Суворова, Учебник