Равенство треугольников
Мы знаем, что две геометрические фигуры считаются равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы, значит, если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
Пример:
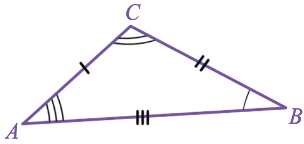
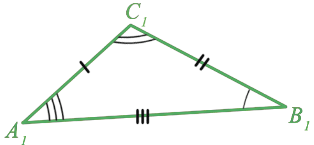
Равенство треугольников ABC и A1B1C1 обозначается так: 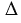 ABC =
ABC = 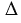 A1B1C1
A1B1C1
В равных треугольниках против соответственно равных сторон лежат равные углы и обратно: против соответственно равных углов лежат равные стороны.
Для примера рассмотрим одну из пар сторон треугольников: BC = B1C1, значит, 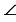 A =
A = 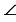 A1 и наоборот: из того что
A1 и наоборот: из того что 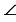 A =
A = 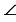 A1, следует, что BC = B1C1.
A1, следует, что BC = B1C1.
Советуем посмотреть:
Первый признак равенства треугольников
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Построения циркулем и линейкой
Правило встречается в следующих упражнениях:
7 класс
Задание 139, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 172, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 179, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 204, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 214, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 821, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 826, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 484, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Задание 909, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник