Второй признак равенства треугольников

Теорема

Пример:

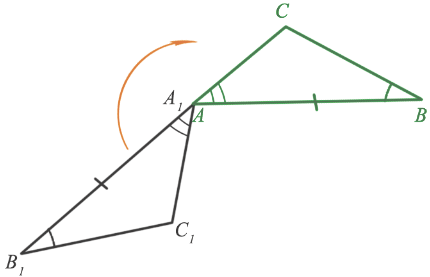
ABC = A₁B₁C₁, так как AB = A₁B₁,  A = A₁, B = B₁.

Доказательство:

Дано: ABC, A₁B₁C₁, AB = A₁B₁,  A = A₁, B = B₁.

Доказать: ABC = A₁B₁C₁

Доказательство:

Рассмотрим ABC и A₁B₁C₁. Наложим их друг на друга так, чтобы совместились: вершины A и A₁ и равные стороны AB и A₁B₁. При этом вершины C и C₁ должны быть по одну сторону от прямой A₁B₁.

Поскольку A = A₁ и B = B₁, то сторона AC наложится на луч A₁C₁, а сторона BC - на луч B₁C₁. Поэтому общая точка сторон  AC и BC, вершина C, окажется лежащей как на луче A₁C₁, так и на луче B₁C₁ и, следовательно, совместится с общей точкой этих лучей - вершиной C₁. Значит, совместятся стороны AC и A₁C₁, BC и B₁C₁.

Таким образом, ABC и A₁B₁C₁ полностью совместятся, поэтому они равны, что и требовалось доказать.