Понятие движения

Осевая симметрия - это отображение плоскости на себя, которое сохраняет расстояния между точками.

Пусть прямая 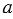- ось симметрии. Возьмем две произвольные точки А и В, которые лежат по одну сторону от оси симметрии, и симметричные относительно прямой 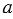им точки А₁ и В₁:

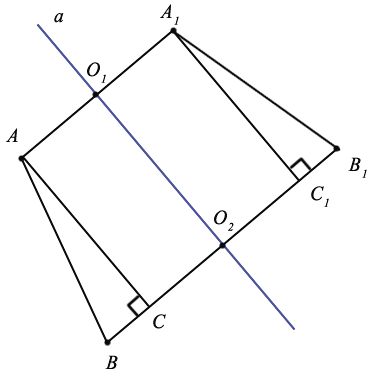
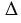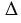Из точек А и А₁ проведем перпендикуляры АС и А₁С₁ к прямой ВВ₁. Рассмотрим АВС и А₁В₁С₁: Они являются прямоугольными. Нам известно, что две прямые перпендикулярные к третьей прямой не пересекаются (т.е. являются параллельными). Значит, из того что АА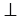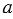₁ и ВВ₁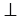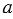, следует, что  то АА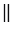₁ВВ₁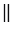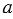, аналогично, АС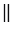А₁С₁. Т.е. мы получили, что в четырехугольнике АСС₁А₁ стороны попарно параллельны, значит, этот четырехугольник является параллелограммом, а, следовательно, АС=А₁С₁. Так как АА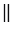₁ВВ₁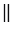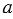, то АО₁=СО₂=О₂С₁=О₁А₁ (данное равенство верно, так как вершины прямоугольника симметричны относительно серединного перпендикуляра, который проведен к его сторонам), поэтому ВС=ВО₂-СО₂=О₂В₁-О₂С₁=С₁В₁. Итак, мы получили, что в рассматриваемых треугольниках АС=А₁С₁ и ВС=С₁В₁, значит, 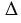АВС=А₁В₁С₁ (по двум катетам). Следовательно, АВ=А₁В₁, то есть расстояние между точками А и В равно расстоянию между симметричными им точками А₁ и В₁.

Рассмотрим случай, когда точки А и В лежат по разные стороны от оси симметрии:

Рассмотрим АО₁О и 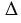А₁О₁О: О₁О - общий катет, АО₁=О₁А₁, т.к. точка А₁ симметрична точке А, следовательн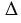о, АО₁О=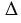А₁О₁О (по двум катетам). Значит, АО=ОА₁. Аналогично находим, что В₁О=ОВ. Поэтому получаем, что АВ=АО+ОВ=ОА₁+В₁О=А₁В₁, т.е. и в данном случае расстояние между точками А и В равно расстоянию между симметричными им точками А₁ и В₁.

При других расположениях точек А, В и А₁, В₁ также получается, что АВ=А₁В₁:

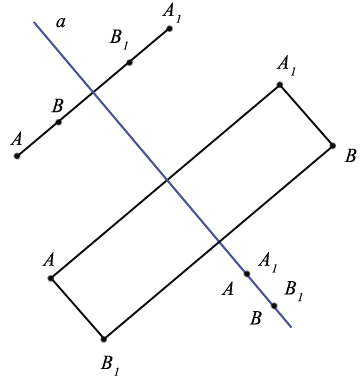
Итак, мы получили, что осевая симметрия является отображением, которое сохраняет расстояния между точками.

Пусть точка О - центр симметрии. Возьмем две произвольные точки А и В и построим точки А₁ и В₁, которые будут симметричны данным относительно точки О:

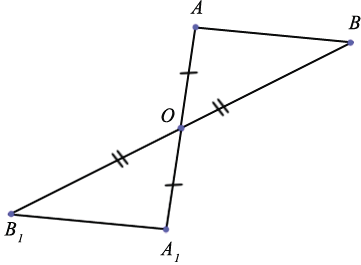
Так как точка А симметрична точке А₁ и В симметрична точке В₁, то А₁О=ОА и В₁О=ОВ. 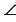АОВ=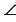В₁ОА₁, так как они вертикальные. Следовательно, 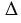АОВ=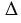В₁ОА₁ (по I признаку равенства треугольников) и АВ=А₁В₁, то есть расстояние между точками А и В равно расстоянию между симметричными им точками А₁ и В₁. Значит, центральная симметрия является отображением, которое сохраняет расстояния между точками.

Любое отображение, которое сохраняет расстояния между точками называется движением (или перемещением).

Движение плоскости - это отображение плоскости на себя, сохраняющее расстояния.

Поясним на примере осевой симметрии, по какой причине отображение, которое сохраняет расстояния, называют движением:

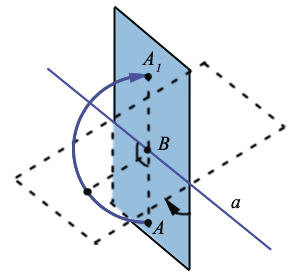
На рисунке видно, что осевую симметрию можно представить как поворот плоскости в пространстве на 180⁰ вокруг оси .

Теорема

Доказательство

Дано: движение, отрезок АВ, А отображается в А₁, В отображается в В₁

Доказать, что отрезок АВ отображается на отрезок А₁В₁

Доказательство:

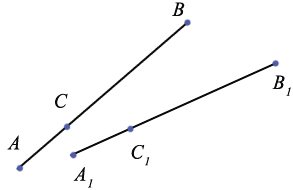
Возьмем произвольную точку С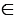АВ, которая отображается в точку С₁.

АВ=АС+СВ.

При движении расстояния сохраняются, поэтому АВ=А₁В₁, АС=А₁С₁ и СВ=С₁В₁. (1)

Из данных равенств имеем, что А₁В₁=АВ=АС+СВ=А₁С₁+С₁В₁, следовательно, С₁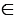А₁В₁ (если предположить обратное, то будет выполнятся неравенство А₁С₁+С₁В₁>A₁B₁). Значит, точки отрезка АВ отображаются в точки отрезка А₁В₁.

Возьмем произвольную точку С₁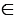А₁В₁, при этом при заданном движении точка С отображается в данную точку С₁. Из соотношений (1) и равенства А₁В₁=А₁С₁+С₁В₁, следует, что АС+СВ=АВ, а, значит, С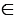АВ. Т.е. в каждую точку С₁ отрезка А₁В₁ отображается какая-нибудь точка С отрезка АВ. Теорема доказана.

Следствие