Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников позволяют сравнивать прямоугольные треугольники лишь по двум элементам, так как любые два прямых угла равны.
1. Признак равенства по двум катетам
| Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны |
Данный признак следует из первого признака равенства треугольников.
Пример:
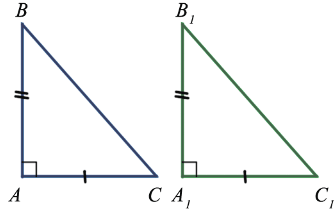
 ABC =
ABC =  A1B1C1, т.к. AB = A1B1 и AC = A1C1.
A1B1C1, т.к. AB = A1B1 и AC = A1C1.
2. Признак равенства по катету и острому углу
| Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны |
Данный признак следует из второго признака равенства треугольников.
Пример:
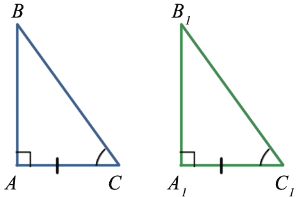
 ABC =
ABC =  A1B1C1, т.к. AC = A1C1,
A1B1C1, т.к. AC = A1C1,  C =
C =  C1
C1
3. Признак равенства по гипотенузе и острому углу
Теорема
| Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого,то такие треугольники равны |
Пример:
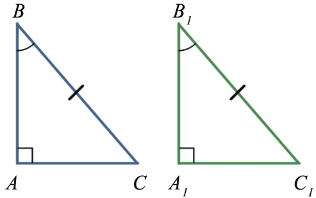
 ABC =
ABC =  A1B1C1, т.к. BC = B1C1,
A1B1C1, т.к. BC = B1C1,  B =
B =  B1
B1
Доказательство
Так как сумма двух острых углов прямоугольного треугольника равна 900, то в таких треугольниках два других острых угла также равны, поэтому данные треугольники равны по второму признаку треугольников, т.е. по стороне(по гипотенузе) и двум прилежащим к ней углам, что и требовалось доказать.
4. Признак равенства по катету и гипотенузе
Теорема
| Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны |
Пример:
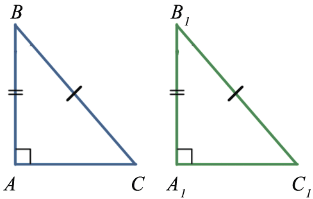
 ABC =
ABC =  A1B1C1, т.к. BC = B1C1, AB = A1B1
A1B1C1, т.к. BC = B1C1, AB = A1B1
Доказательство
Дано:  ABC,
ABC,  A1B1C1, BC = B1C1, AB = A1B1
A1B1C1, BC = B1C1, AB = A1B1
Доказать:  ABC =
ABC =  A1B1C1
A1B1C1
Доказательство:
Рассмотрим данные треугольники:

Так как  A =
A =  A1, то
A1, то  ABC можно наложить на
ABC можно наложить на  A1B1C1 так, что вершина A совместится с вершиной A1, а стороны AC и AB наложатся соответственно на лучи A1C1 и A1B1. При этом вершина B совместится с вершиной B1, потому что AB = A1B1. Но тогда вершина C также совместится с вершиной C1. Действительно, если предположить, что точка C совместится с некоторой другой точкой C2 луча A1C1, то получим равнобедренный треугольник C1B1C2.
A1B1C1 так, что вершина A совместится с вершиной A1, а стороны AC и AB наложатся соответственно на лучи A1C1 и A1B1. При этом вершина B совместится с вершиной B1, потому что AB = A1B1. Но тогда вершина C также совместится с вершиной C1. Действительно, если предположить, что точка C совместится с некоторой другой точкой C2 луча A1C1, то получим равнобедренный треугольник C1B1C2.
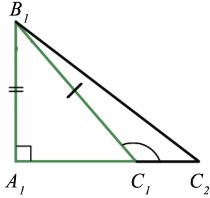
В  C1B1C2 углы при основании не равны (
C1B1C2 углы при основании не равны ( C2 - острый, а
C2 - острый, а  C1 - тупой, так как он смежный с углом B1C1A1, который является острым). А это невозможно, так как у равнобедренного треугольника углы у основания равны, следовательно, вершина C совместится с вершиной C1. А это значит, что полностью совместятся треугольники ABC, A1B1C1, т.е. они равны, что и требовалось доказать.
C1 - тупой, так как он смежный с углом B1C1A1, который является острым). А это невозможно, так как у равнобедренного треугольника углы у основания равны, следовательно, вершина C совместится с вершиной C1. А это значит, что полностью совместятся треугольники ABC, A1B1C1, т.е. они равны, что и требовалось доказать.
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Некоторые свойства прямоугольных треугольников
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Построение треугольника по трем его сторонам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 275, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 443, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 644, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 823, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 836, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 839, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1207, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 453, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник