Сравнение отрезков

Одной из простейших геометрических фигур является отрезок. Для того чтобы сравнивать отрезки, можно использовать два способа: 

1. Метод наложения.
2. Измерение длин.

Метод наложения:

Пусть нам даны два отрезка AB и СD:

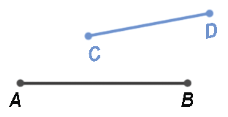
Совместим начало отрезка AB и СD (точки A и С).

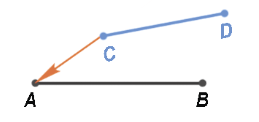
Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.

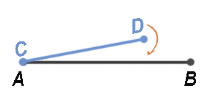
Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.

Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.

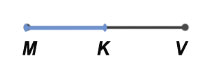
MK = KV, K - середина отрезка.

Рассмотрим еще одну пару отрезков HG и ST.

Совместим начало отрезка HG и ST.

Затем повернем отрезок ST так, чтобы он совпал с отрезком HG.

В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.

Вывод:

Измерение длин:

Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков. 

Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.

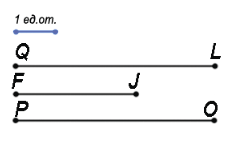
Наложим единичный отрезок на данные.

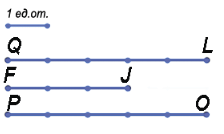
Посчитаем, какое количество  единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ  = 3 ед.от., PO = 5 ед. от.

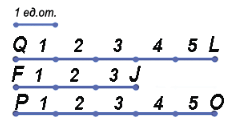
Сравним отрезки: QL > FJ (т.к. 5 > 3), FJ < PO (т.к. 3 < 5), QL = PO (т.к. 5 = 5).

• Если при наложении отрезков оба их конца совмещаются, значит отрезки равны.
• Если при измерении отрезков их длины равны, то отрезки равны.