Поворот

Пусть О - точка на плоскости, 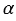- угол поворота.

Поворот плоскости вокруг точки О на угол 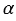- это отображение плоскости на себя, при котором каждая точка Е отображается в такую точку Е₁, что ОЕ = ОЕ₁ и  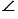ЕОЕ₁ =  .

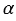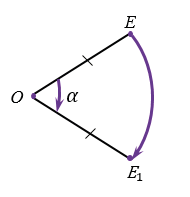
При повороте плоскости вокруг точки О сама точка О остается на месте, т.е. отображается сама в себя, а все остальные точки поворачиваются вокруг точки О в одном и том же направлении - по часовой стрелке (как на рисунке выше) или против часовой стрелки.

Доказательство

Дано: О - центр поворота, 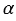- угол поворота по часовой стрелке (случай поворота против часовой стрелки рассматривается аналогично), точки Е и К отображаются при повороте в точки Е₁ и К₁.

Доказать: поворот - движение.

Доказательство:

1 случай

Точки О, Е и К не лежат на одной прямой.

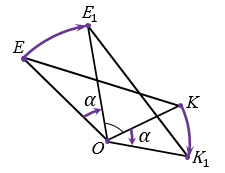
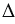ОЕК = 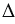ОЕ₁К₁ по двум сторонам и углу между ними (ОЕ = ОЕ₁, ОК = ОК₁, т.к. Е и К отображаются при повороте в Е₁ и К₁, 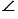ЕОК = 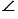Е₁ОК₁ = 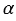+ Е₁ОК). В равных треугольниках элементы соответственно равны поэтому ЕК = Е₁К₁, т.е. расстояние между точками Е и К равно расстоянию между точками Е₁ и К₁. Значит, поворот сохраняет расстояния между точками и поэтому является частным случаем движения.

2 случай

Точки О, Е и К лежат на одной прямой.

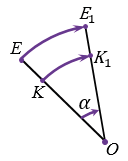
ЕК = ОЕ - ОК и Е₁К₁ = ОЕ₁ - ОК₁, при этом ОЕ = ОЕ₁, ОК = ОК₁, т.к. Е и К отображаются при повороте в Е₁ и К₁, следовательно, ЕК = Е₁К₁, т.е. расстояние между точками Е и К равно расстоянию между точками Е₁ и К₁. Значит, поворот сохраняет расстояния между точками и поэтому является частным случаем движения.

Пример

Построить А₁В₁С₁, который получается из АВС поворотом вокруг точки О по часовой стрелке на угол .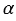

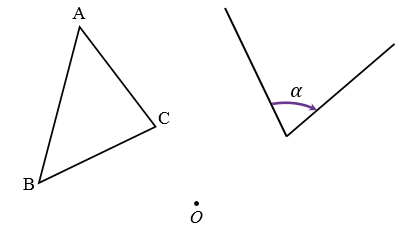
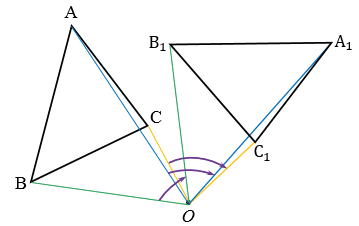
Построим точки А₁, В₁ и С₁, которые получаются из точек А, В и С поворотом вокруг точки О по часовой стрелке на угол 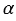. Соединяя попарно точки А₁, В₁, С₁ отрезками, получим искомый 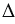А₁В₁С₁.