Функция y=k/x и её график.
Мы знаем, что обратная пропорциональность - это зависимость, которая характеризуется тем, что с увеличением (уменьшением) одной величины в несколько раз другая величина уменьшается (увеличивается) во столько же раз.
Рассмотрим задачи:
1. Пешеход движется из пункта А в пункт В, расстояние между которыми рано 15 км. Пусть его скорость равна  км/ч, а время движения -
км/ч, а время движения - 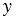 ч.
ч.
Зависимость переменной 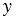 от переменной
от переменной  является обратной пропорциональностью: увеличение скорости
является обратной пропорциональностью: увеличение скорости  в несколько раз приводит к уменьшению времени движения во столько же раз, и наоборот, уменьшение скорости движения приводит к увеличению времени движения во столько же раз. Этой функциональной зависимости соответствует функция, которая задана формулой
в несколько раз приводит к уменьшению времени движения во столько же раз, и наоборот, уменьшение скорости движения приводит к увеличению времени движения во столько же раз. Этой функциональной зависимости соответствует функция, которая задана формулой 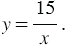
2. Пусть нам дан прямоугольник длина которого равна  м, а ширина
м, а ширина 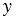 м, Известно, что его площадь равна 4 м2.
м, Известно, что его площадь равна 4 м2.
Зависимость переменной 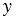 от переменной
от переменной  является обратной пропорциональностью: увеличение длины
является обратной пропорциональностью: увеличение длины  в несколько раз приводит к уменьшению ширины прямоугольника во столько же раз, и наоборот, уменьшение длины приводит к увеличению ширины во столько же раз. Этой функциональной зависимости соответствует функция, которая задана формулой
в несколько раз приводит к уменьшению ширины прямоугольника во столько же раз, и наоборот, уменьшение длины приводит к увеличению ширины во столько же раз. Этой функциональной зависимости соответствует функция, которая задана формулой 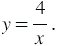
Общей математической моделью этих и многих других реальных процессов является функция, которая задается формулой 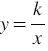 .
.
Функцию, которую можно задать формулой вида 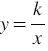 , где , где 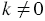 , называют обратной пропорциональностью. , называют обратной пропорциональностью. |
Областью определения функции 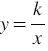 являются все числа, кроме 0, так как в выражении
являются все числа, кроме 0, так как в выражении 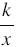 допустимыми значениями переменной
допустимыми значениями переменной  являются все числа кроме 0.
являются все числа кроме 0.
Рассмотрим функцию 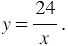 Приведем некоторые значения аргумента и соответствующие им значения функции. Сначала возьмем несколько положительных значений аргумента, а затем несколько противоположных им отрицательных значений.
Приведем некоторые значения аргумента и соответствующие им значения функции. Сначала возьмем несколько положительных значений аргумента, а затем несколько противоположных им отрицательных значений.
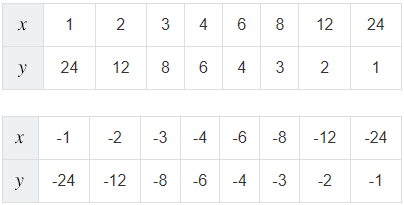
Далее на координатной плоскости отметим точки, координаты ( ;
; 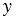 ) которых приведены в таблице (рис. 1).
) которых приведены в таблице (рис. 1).
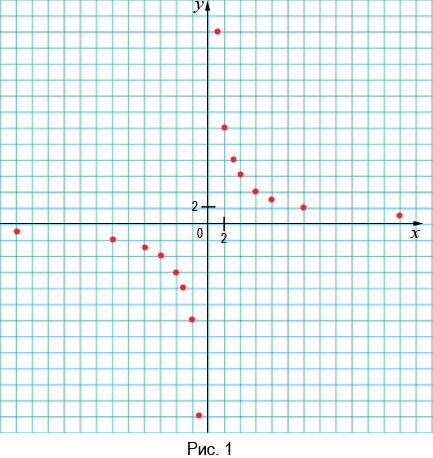
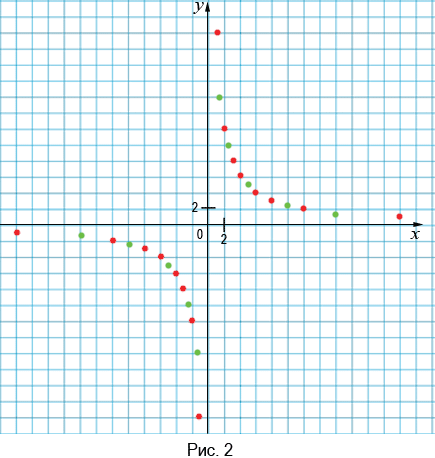
Отмечая больше точек, координаты которых удовлетворяют уравнению 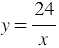 , будем получать фигуру (рис. 2), которая будет все меньше отличаться от графика функции
, будем получать фигуру (рис. 2), которая будет все меньше отличаться от графика функции 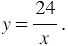
При этом, сколько бы мы точек не отметили ни одна из них не будет иметь абсциссу равную нулю, так как 0 не принадлежит области определения данной функции, а значит, график функции  не будет иметь общих точек с осью ординат. А также график данной функции не будет иметь общих точек с осью абсцисс, то есть точек, у которых ординаты будут равны нулю, так как уравнение не имеет решений. Из чего делаем вывод, что число 0 не принадлежит области значений данной функции. Заметим, что областью значений данной функции являются все числа, кроме 0. Если
не будет иметь общих точек с осью ординат. А также график данной функции не будет иметь общих точек с осью абсцисс, то есть точек, у которых ординаты будут равны нулю, так как уравнение не имеет решений. Из чего делаем вывод, что число 0 не принадлежит области значений данной функции. Заметим, что областью значений данной функции являются все числа, кроме 0. Если  > 0, то
> 0, то  > 0; если
> 0; если  < 0, то
< 0, то 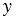 < 0. Следовательно, точки графика данной функции могут находиться только в I и III координатных четвертях.
< 0. Следовательно, точки графика данной функции могут находиться только в I и III координатных четвертях.
Заметим, что если бы 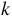 <0, то если
<0, то если  > 0, то
> 0, то 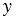 < 0; если
< 0; если  < 0, то
< 0, то 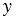 > 0. Следовательно, точки графика функции должны находится только в II и IV координатных четвертях.
> 0. Следовательно, точки графика функции должны находится только в II и IV координатных четвертях.
При этом если модуль абсциссы увеличивается, то расстояния от точек графика функции 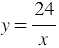 до оси абсцисс уменьшаются и могут стать сколь угодно малыми, но никогда не станут равными нулю. Аналогично: с уменьшением модуля абсциссы расстояния от точек графика до оси ординат уменьшаются и могут стать сколь угодно малыми, но никогда не будут равны нулю.
до оси абсцисс уменьшаются и могут стать сколь угодно малыми, но никогда не станут равными нулю. Аналогично: с уменьшением модуля абсциссы расстояния от точек графика до оси ординат уменьшаются и могут стать сколь угодно малыми, но никогда не будут равны нулю.
Если мы отметим на координатной плоскости все точки, координаты которых удовлетворяют уравнению 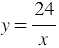 , то мы получим фигуру, которая изображена на рисунке 3.
, то мы получим фигуру, которая изображена на рисунке 3.
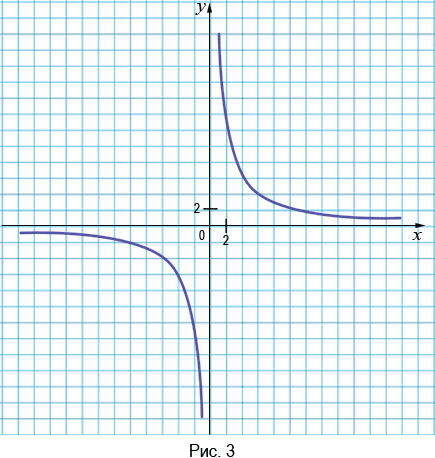
Данную фигуру называют гиперболой, она является графиком функции 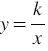 , где
, где 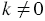 . Гипербола состоит из двух частей, которые называются ветвями гиперболы.
. Гипербола состоит из двух частей, которые называются ветвями гиперболы.
Противоположным значениям аргумента соответствуют противоположные значения функции. Действительно, в рассматриваемой функции 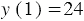 , а
, а 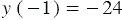 , то есть
, то есть 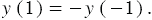 Или в общем виде
Или в общем виде 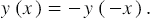 То есть если точка
То есть если точка 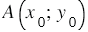 , где
, где 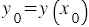 , принадлежит гиперболе
, принадлежит гиперболе 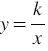 , то и точка
, то и точка 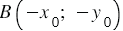 , которая симметрична точке
, которая симметрична точке 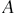 относительно начала координат, также принадлежит этой гиперболе. То есть гипербола
относительно начала координат, также принадлежит этой гиперболе. То есть гипербола 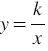 является симметричной фигурой с центром симметрии в точке О(0; 0). Функцию, которая обладает таким свойством, называют нечётной.
является симметричной фигурой с центром симметрии в точке О(0; 0). Функцию, которая обладает таким свойством, называют нечётной.
Пример: Решим уравнение 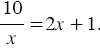
Решим данное уравнение с помощью графического метода, для этого рассмотрим функции 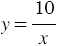 и
и 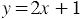 . Построим графики данных функций на одной координатной плоскости (рис. 4).
. Построим графики данных функций на одной координатной плоскости (рис. 4).
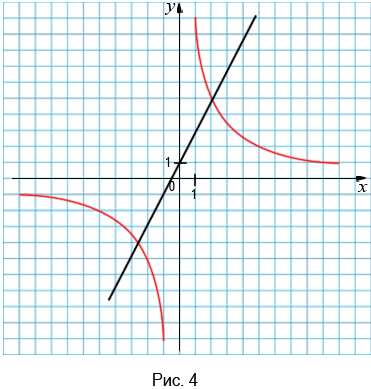
Графики данных функций пересекаются в двух точках, абсциссы которых равны 2 и 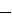 2,5. В каждой из точек пересечения графиков функций значение функции
2,5. В каждой из точек пересечения графиков функций значение функции 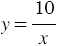 равно значению функции
равно значению функции 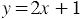 . То есть, при найденных абсциссах значения выражений
. То есть, при найденных абсциссах значения выражений 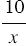 и
и 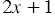 равны, то есть числа 2 и
равны, то есть числа 2 и 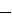 2,5 являются корнями уравнения
2,5 являются корнями уравнения 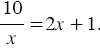
Советуем посмотреть:
Основное свойство рациональной дроби
Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями
Умножение и деление рациональных дробей. Возведение рациональной дроби в степень
Равносильные уравнения. Рациональные уравнения
Степень с целым отрицательным показателем
Свойства степени с целым показателем
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 322, Мерзляк, Полонский, Якир, Учебник
Номер 323, Мерзляк, Полонский, Якир, Учебник
Номер 332, Мерзляк, Полонский, Якир, Учебник
Номер 10, Мерзляк, Полонский, Якир, Учебник
Номер 653, Мерзляк, Полонский, Якир, Учебник
Номер 800, Мерзляк, Полонский, Якир, Учебник
Упражнение 266, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1144, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1242, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение стр. 52, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс