Свойства степени с целым показателем
1) Для любого 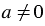 и любых целых
и любых целых 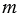 и
и 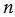 выполняются равенства:
выполняются равенства:
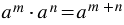 , то есть при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.
, то есть при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.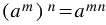 , то есть при возведении степени в степень показатели перемножают, а основание оставляют прежним.
, то есть при возведении степени в степень показатели перемножают, а основание оставляют прежним.
Равенство 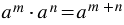 называют основным свойством степени.
называют основным свойством степени.
2) Для любых 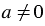 и
и 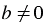 и любого целого
и любого целого 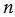 выполняется равенство:
выполняется равенство: 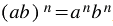 , то есть при возведении произведения в степень каждый множитель возводят в эту степень и полученные результаты перемножают.
, то есть при возведении произведения в степень каждый множитель возводят в эту степень и полученные результаты перемножают.
3) Для любого 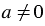 и любых целых
и любых целых 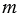 и
и 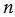 выполняется равенство:
выполняется равенство: 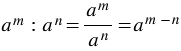 , то есть при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя, при этом учитываем то, что деление можно заменить дробью (делимое - числитель, делитель - знаменатель).
, то есть при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя, при этом учитываем то, что деление можно заменить дробью (делимое - числитель, делитель - знаменатель).
4) Для любых 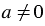 и
и 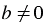 и любого целого
и любого целого 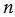 выполняется равенство:
выполняется равенство: 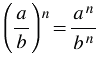 , то есть при возведении дроби в степень в эту степень возводят и числитель и знаменатель.
, то есть при возведении дроби в степень в эту степень возводят и числитель и знаменатель.
Примеры:
1) Представьте выражение в виде степени с основанием 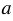 :
:
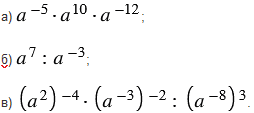
Решение:
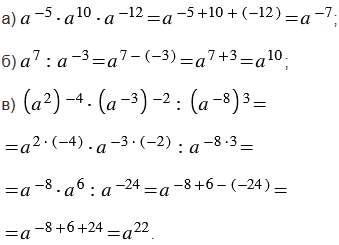
2) Найдите значение выражения:
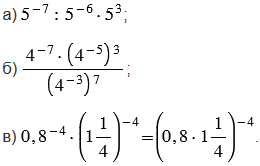
Решение:
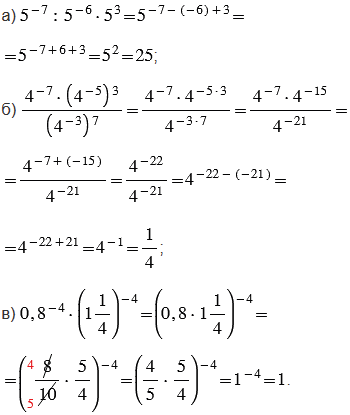
3) Упростите выражение:
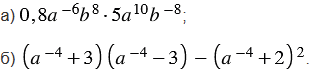
Решение:
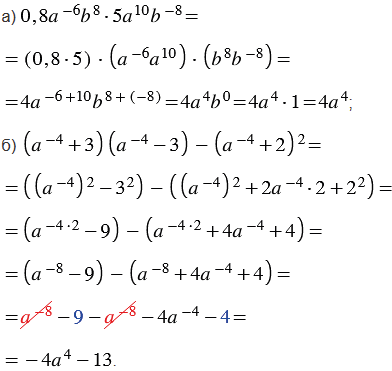
4) Выполните вычисления и результат запишите в стандартном виде:
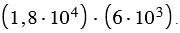
Решение:
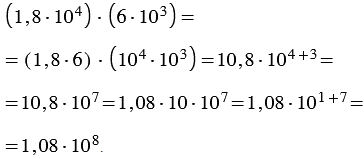
Советуем посмотреть:
Основное свойство рациональной дроби
Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями
Умножение и деление рациональных дробей. Возведение рациональной дроби в степень
Равносильные уравнения. Рациональные уравнения
Степень с целым отрицательным показателем
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 1, Мерзляк, Полонский, Якир, Учебник
Номер 274, Мерзляк, Полонский, Якир, Учебник
Номер 292, Мерзляк, Полонский, Якир, Учебник
Упражнение 1194, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1198, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1214, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1215, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1226, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1260, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1268, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс