Основное свойство рациональной дроби
Ранее мы познакомились с такими понятиями как тождественно равные выражения и тождества. Эти понятия используют и при работе с рациональными дробями, только их следует уточнить.
| Выражения, соответствующие значения которых равны при любых допустимых значениях входящих в них переменных, называют тождественно равными. |
| Равенство, которое выполняется при любых допустимых значениях входящих в него переменных, называют тождеством. |
Так, например, равенство 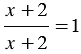 является тождеством, так как оно выполняется при всех допустимых значениях
является тождеством, так как оно выполняется при всех допустимых значениях 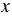 , то есть при всех
, то есть при всех 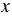 , кроме
, кроме 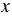 =
= 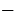 2.
2.
Тождественные преобразования дробных выражений
Вам уже известно основное свойство обыкновенной дроби, согласно которому при умножении и делении числителя и знаменателя дроби на одно и то же отличное от нуля число получается дробь, равная данной. Иначе говоря, при любых натуральных значениях 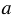 ,
, 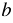 и
и 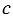 верно равенство
верно равенство 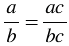 , где
, где 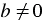 и
и 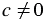 .
.
Аналогичным свойством обладают и рациональные дроби:
| Если числитель и знаменатель рациональной дроби умножить или разделить на один и тот же ненулевой многочлен, то получится дробь, тождественно равная данной. |
Это свойство называют основным свойством рациональные дроби. С помощью букв его записывают так:
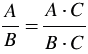 , где
, где 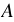 ,
, 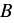 и
и 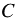 - многочлены, причем
- многочлены, причем 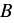 и
и 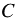 ненулевые многочлены.
ненулевые многочлены.
Пример 1. Приведите дробь 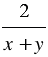 к новому знаменателю
к новому знаменателю 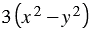 .
.
Решение: Согласно формуле разности квадратов двух выражений 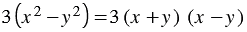 , то новый знаменатель отличается от исходного множителем
, то новый знаменатель отличается от исходного множителем  .
.
Значит, числитель и знаменатель дроби 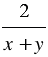 надо умножить на дополнительный множитель
надо умножить на дополнительный множитель  :
:
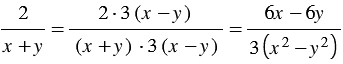 .
.
Следствия из основного свойства рациональной дроби:
1) Замену выражения 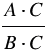 на тождественно равную ему дробь на тождественно равную ему дробь 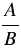 называют сокращением дроби на множитель называют сокращением дроби на множитель 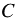 , где , где 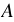 , , 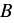 и и 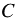 многочлены, причем многочлены, причем 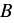 и и 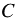 - ненулевые многочлены. - ненулевые многочлены. |
Пример 2. Сократим дробь 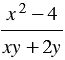 .
.
Решение: Разложим на множители числитель и знаменатель данной дроби. В числителе применяем формулу разности квадратов двух выражений, в знаменателе выносим за скобки общий множитель 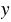 :
:
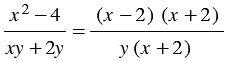 .
.
Сократим полученную дробь на общий множитель 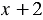 , получим:
, получим:
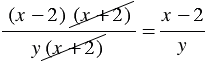 .
.
Дальнейшее сокращение дроби невозможно, следовательно, получаем:
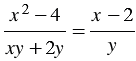 .
.
2) Если и числитель, и знаменатель дроби заменить на противоположные выражения, то получится дробь, равная данной, то есть 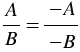 , где , где 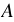 и и 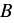 - многочлены, причем - многочлены, причем 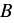 ненулевой многочлен. ненулевой многочлен. |
Пример 3. Преобразуем дробь 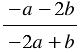 , заменив двучлены в числителе и знаменателе на противоположные:
, заменив двучлены в числителе и знаменателе на противоположные:
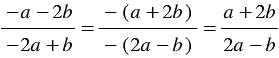 .
.
3) Если числитель или знаменатель дроби заменить на противоположное выражение и при этом поменять знак перед дробью, то получится дробь, равная данной, то есть 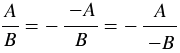 , где , где 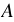 и и 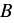 - многочлены, причем - многочлены, причем 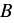 ненулевой многочлен. ненулевой многочлен. |
Пример 4. Сократим дробь 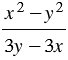 .
.
Решение: Разложим на множители числитель и знаменатель данной дроби. В числителе применяем формулу разности квадратов двух выражений, в знаменателе выносим за скобки общий множитель 3:
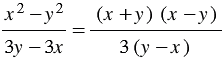 .
.
Множители 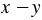 и
и 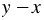 "почти одинаковы" - они отличаются только знаками. Чтобы дробь можно было сократить, заменим, например, выражение
"почти одинаковы" - они отличаются только знаками. Чтобы дробь можно было сократить, заменим, например, выражение 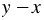 в знаменателе дроби на
в знаменателе дроби на 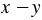 и при этом поставим знак "минус" перед дробью:
и при этом поставим знак "минус" перед дробью:
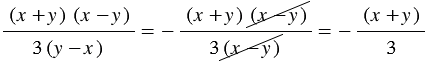 .
.
Дальнейшее сокращение дроби невозможно, следовательно, получаем:
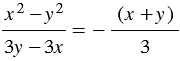 .
.
Советуем посмотреть:
Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями
Умножение и деление рациональных дробей. Возведение рациональной дроби в степень
Равносильные уравнения. Рациональные уравнения
Степень с целым отрицательным показателем
Свойства степени с целым показателем
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 108, Мерзляк, Полонский, Якир, Учебник
Номер 790, Мерзляк, Полонский, Якир, Учебник
Номер 798, Мерзляк, Полонский, Якир, Учебник
Номер 827, Мерзляк, Полонский, Якир, Учебник
Номер 852, Мерзляк, Полонский, Якир, Учебник
Упражнение 65, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 152, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 429, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 821, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 1012, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс