Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Прямоугольник - это четырехугольник, у которого все углы прямые.
На рис. 1 изображен прямоугольник АВСD.
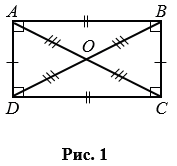
Отрезки АВ и СD, АD и ВС - противолежащие стороны прямоугольника. Противолежащие стороны прямоугольника не имеют общих точек. В прямоугольнике противолежащие стороны равны, тогда на рис. 1 в прямоугольнике АВСD: АВ = DС, АD = ВС.
Отрезки АВ и АD, АD и DC, DC и ВС, АВ и ВС - соседние или смежные стороны. Смежные стороны - стороны, которые имеют общую вершину. Смежные стороны прямоугольника имеют специальные названия: длина и ширина.
Отрезки АС и ВD - диагонали прямоугольника. Диагонали прямоугольника соединяют противолежащие вершины. Диагонали прямоугольника равны и точкой пересечения делятся пополам. Так на рис. 1 АС = ВD и ОА = ОВ = ОС = ОD.
Периметр - это сумма длин всех сторон многоугольника. Обозначается периметр буквой 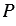 .
.
Учитывая, что в прямоугольнике противоположные стороны равны, его периметр вычисляется по формуле: 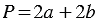 или
или 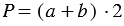 , где
, где 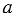 и
и 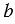 смежные стороны прямоугольника (длина и ширина).
смежные стороны прямоугольника (длина и ширина).
Площадь прямоугольника обозначается буквой 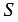 . Площадь прямоугольника равна произведению его смежных сторон, т.е. если
. Площадь прямоугольника равна произведению его смежных сторон, т.е. если 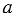 и
и 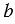 смежные стороны прямоугольника, то его площадь
смежные стороны прямоугольника, то его площадь 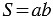 .
.
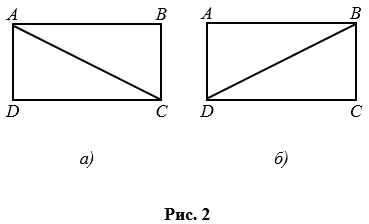
Каждая диагональ прямоугольника делит его на два равных треугольника. На рис. 2, 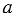 диагональ АС делит прямоугольник АВСD на два равных треугольника АВС и АDС, т.е.
диагональ АС делит прямоугольник АВСD на два равных треугольника АВС и АDС, т.е. 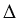 АВС =
АВС = 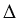 АDС, а на рис. 2, б диагональ ВD делит прямоугольник АВСD на два равных треугольника ВАD и ВСD, т.е.
АDС, а на рис. 2, б диагональ ВD делит прямоугольник АВСD на два равных треугольника ВАD и ВСD, т.е.
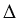 ВАD =
ВАD = 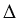 ВСD.
ВСD.
Прямоугольник, у которого все стороны равны, называют квадратом.
Ось симметрии
Прямоугольник имеет ось симметрии. Ось симметрии прямоугольника - это прямая, проходящая через средины противоположных сторон прямоугольника. У прямоугольника две оси симметрии, на рис. 3 прямые 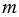 и
и 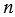 оси симметрии прямоугольника АВСD.
оси симметрии прямоугольника АВСD.
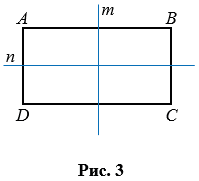
Если лист бумаги перегнуть по прямым 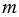 (или
(или 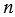 ), то две части прямоугольника, лежащие по разные стороны от прямой
), то две части прямоугольника, лежащие по разные стороны от прямой 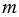 (или
(или 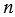 ), совпадут.
), совпадут.
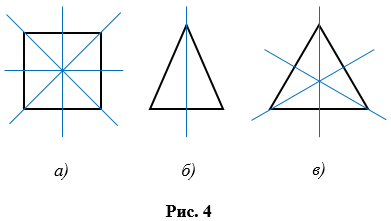
Существуют и другие фигуры, которые имеют ось симметрии, такие фигуры называют симметричными относительно прямой. Так, например, квадрат имеет четыре оси симметрии (рис. 4, 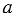 ), равнобедренный треугольник одну ось симметрии (рис. 4, б), а равносторонний треугольник - три оси симметрии (рис.4, в).
), равнобедренный треугольник одну ось симметрии (рис. 4, б), а равносторонний треугольник - три оси симметрии (рис.4, в).
Советуем посмотреть:
Единицы измерения площадей. Свойства площадей
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Измерение углов. Транспортир. Виды углов
Правило встречается в следующих упражнениях:
5 класс
Задание 312, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 717, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 757, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1437, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2.83, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 3.209, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.47, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.101, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.112, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 1, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 123, Мерзляк, Полонский, Якир, Учебник
Номер 327, Мерзляк, Полонский, Якир, Учебник
Номер 762, Мерзляк, Полонский, Якир, Учебник
Номер 769, Мерзляк, Полонский, Якир, Учебник
Задание 725, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 856, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1398, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1493, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 5.78, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Номер 20, Мерзляк, Полонский, Якир, Учебник
Номер 379, Мерзляк, Полонский, Якир, Учебник
Номер 663, Мерзляк, Полонский, Якир, Учебник
Упражнение 53, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 258, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 359, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 718, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 803, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 817, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 915, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 450, Мерзляк, Полонский, Якир, Учебник
Упражнение 179, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 523, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 527, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 560, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 564, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 572, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 757, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 890, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 264, Макарычев, Миндюк, Учебник
9 класс