Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Мы знаем правило сложения и вычитания обыкновенных дробей с одинаковыми знаменателями. Рациональные дроби с одинаковыми знаменателями складывают и вычитают аналогично.
|
Чтобы сложить рациональные дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Чтобы вычесть рациональные дроби с одинаковыми знаменателями, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же.
|
Пример 1. Выполните вычитание рациональных дробей:
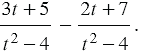
Используя правило вычитания рациональных дробей, запишем:
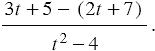
Далее раскроем скобки в числителе полученной дроби:
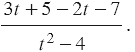
В числителе приводим подобные слагаемые, а в знаменателе раскладываем на множители разность квадратов, получаем:
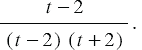
Мы видим, что числитель и знаменатель содержат общий ненулевой многочлен 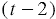 , а значит, данную дробь мы можем сократить на данный многочлен, получаем, что:
, а значит, данную дробь мы можем сократить на данный многочлен, получаем, что:
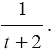
Пример 2. Выполните сложение рациональных дробей.

Если мы внимательно рассмотрим знаменатели, то заметим, что знаменатель первой дроби является выражением противоположным выражению, которое стоит в знаменателе второй дроби, то есть 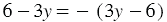 , поэтому мы можем записать, что:
, поэтому мы можем записать, что:
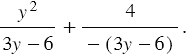
Используя основное свойство дроби, мы можем переписать наше выражение в следующем виде:
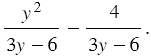
Далее выполняем вычитание, используя правило вычитание рациональных дробей:
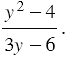
Мы видим, что в числителе дроби находится разность квадратов, поэтому мы можем разложить его на множители, а в знаменателе вынести общий множитель 3, получим:
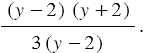
Мы видим, что числитель и знаменатель содержат общий ненулевой многочлен 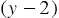 , а значит, данную дробь мы можем сократить на данный многочлен, получаем, что:
, а значит, данную дробь мы можем сократить на данный многочлен, получаем, что:
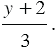
Советуем посмотреть:
Основное свойство рациональной дроби
Сложение и вычитание рациональных дробей с разными знаменателями
Умножение и деление рациональных дробей. Возведение рациональной дроби в степень
Равносильные уравнения. Рациональные уравнения
Степень с целым отрицательным показателем
Свойства степени с целым показателем
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 85, Мерзляк, Полонский, Якир, Учебник
Номер 107, Мерзляк, Полонский, Якир, Учебник
Номер 8, Мерзляк, Полонский, Якир, Учебник
Номер 187, Мерзляк, Полонский, Якир, Учебник
Номер 8, Мерзляк, Полонский, Якир, Учебник
Номер 210, Мерзляк, Полонский, Якир, Учебник
Упражнение 56, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 58, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 66, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 71, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс
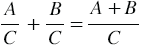 , где
, где 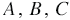 многочлены, причём многочлен
многочлены, причём многочлен 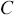 - ненулевой.
- ненулевой.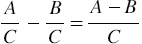 , где
, где