Сложение и вычитание рациональных дробей с разными знаменателями
Чтобы сложить или вычесть рациональные дроби с разными знаменателями, нужно сначала привести эти дроби к общему знаменателю, после чего воспользоваться правилами сложения или вычитания рациональных дробей с одинаковыми знаменателями.
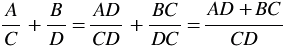 или
или 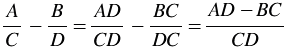 , где
, где 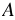 ,
, 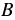 ,
, 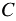 и
и 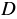 - многочлены, причём многочлены
- многочлены, причём многочлены 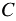 и
и 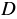 - ненулевые.
- ненулевые.
Здесь в качестве общего знаменателя выбрано выражение, равное произведению знаменателей данных дробей. Но произведение знаменателей данных дробей не всегда является наиболее удобным общим знаменателем. Помним, что при нахождении общего знаменателя обыкновенных дробей мы находили наименьшее общее кратное знаменателей, раскладывая их на простые множители. Аналогично для нахождения общего знаменателя рациональных дробей может оказаться удобным предварительно разложить знаменатели на множители.
Пример 1. Найдите сумму дробей 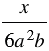 и
и 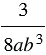 .
.
Решение:
Знаменатели дробей представляют собой одночлены. Наиболее простым общим знаменателем является одночлен 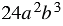 . Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей складываемых дробей, а каждая переменная взята с наибольшим показателем степени, с которым она входит в знаменатели дробей. Тогда дополнительным множителем к первой дроби будет одночлен
. Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей складываемых дробей, а каждая переменная взята с наибольшим показателем степени, с которым она входит в знаменатели дробей. Тогда дополнительным множителем к первой дроби будет одночлен 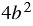 , ко второй дроби - одночлен
, ко второй дроби - одночлен 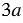 . Получаем:
. Получаем:
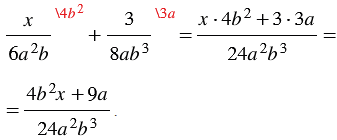
Пример 2. Найдите разность дробей 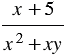 и
и 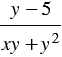 .
.
Решение:
Чтобы найти общий знаменатель вычитаемых дробей, разложим знаменатель каждой дроби на множители:
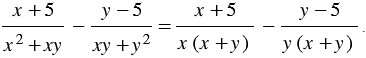
Простейшим общим знаменателем служит выражение 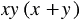 . Тогда дополнительный множитель к первой дроби -
. Тогда дополнительный множитель к первой дроби - 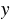 , ко второй дроби -
, ко второй дроби - 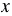 . Получаем:
. Получаем:
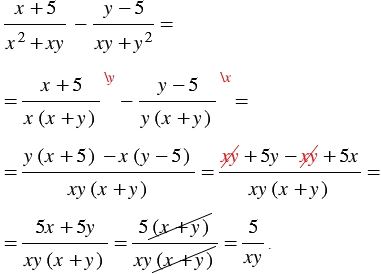
Пример 3. Упростите выражение 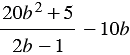 .
.
Решение:
Представим выражение 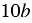 в виде дроби со знаменателем 1 и выполним вычитание дробей, учитывая то, что простейшим общим знаменателем дробей будет выражение
в виде дроби со знаменателем 1 и выполним вычитание дробей, учитывая то, что простейшим общим знаменателем дробей будет выражение 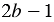 . Получаем:
. Получаем:
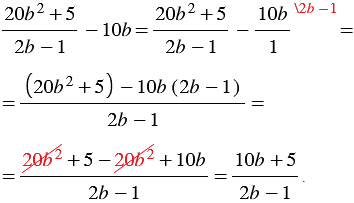
Обратите внимание, сумма и разность двух рациональных дробей являются рациональными дробями.
Советуем посмотреть:
Основное свойство рациональной дроби
Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Умножение и деление рациональных дробей. Возведение рациональной дроби в степень
Равносильные уравнения. Рациональные уравнения
Степень с целым отрицательным показателем
Свойства степени с целым показателем
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Квадратные корни. Дейстительные числа
Системы линейных уравнений с двумя переменными
Элементы математической логики
Правило встречается в следующих упражнениях:
8 класс
Номер 99, Мерзляк, Полонский, Якир, Учебник
Номер 104, Мерзляк, Полонский, Якир, Учебник
Номер 120, Мерзляк, Полонский, Якир, Учебник
Номер 9, Мерзляк, Полонский, Якир, Учебник
Номер 11, Мерзляк, Полонский, Якир, Учебник
Номер 178, Мерзляк, Полонский, Якир, Учебник
Номер 182, Мерзляк, Полонский, Якир, Учебник
Номер 856, Мерзляк, Полонский, Якир, Учебник
Упражнение 75, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 236, Макарычев, Миндюк, Нешков, Суворова, Учебник
9 класс